Yekta (Rauf), La musique turque, 1922 [1]

Détails
Catégorie : Musique
Affichages : 7279

Rauf Yekta (1871-1935), né à Istanbul, est le fondateur de l'ethnomusicologie en Turquie. Outre le Turc, il parlait l'Arabe, le Persan et le Français. Nous reproduisons, en 4 parties, l'intégralité de son article consacré à la musique turque et publié en Français en 1922.

Cet article, la première synthèse moderne sur la musique turque, fut écrit en 1913 et publié dans l'Encyclopédie de la musique et dictionnaire du Conservatoire, édité par Albert Lavignac, première partie, Volume V, pp. 2945–3064. Paris, 1922.

C'est un article très érudit qui évoque la musique dite orientale, ses caractéristiques, la musique turque, les instruments de musique et les rythmes, les makams etc Il cite et discute de nombreuses sources turques, arabes, iraniennes ou européennes.

Rauf Yekta publia également de nombreux articles dans la "Revue musicale" en 1907 et 1908 :

Par la suite, il recueillit avec d'autres, des oeuvres de musique traditionnelle artistique. En 1931, il dirigea l'Association de la musique populaire. Il jouait également du ney.

*************

La musique turque par Raouf Yekta Bey, chef du bureau du Divan (Sublime Porte), Constantinople
Introduction historique et critique. 


Nous avons indiqué la pagination entre crochets [ ].

[2945]

Avant d'aborder directement les principes, sur lesquels est basée la musique turque, j'ai jugé à propos de présenter la critique de certaines idées et hypothèses émises jusqu'à présent sur cette musique par les auteurs occidentaux, ainsi que, les principales questions dont la connaissance est utile pour avoir une idée exacte et complète sur le sujet.

I  De la musique occidentale et de la musique orientale

Si un musicologue de notre temps parcourt les pays civilisés dans le but d'étudier la musique des diverses nations de ces pays, — abstraction faite de la divergence de langue et de l'exigence des manières de s'exprimer particulières à chaque nation, et en considérant strictement les bases fondamentales sur lesquelles repose la musique de ces nations — ce musicologue constate que chez ces peuples il y a essentiellement deux sortes de musique :

1° La musique occidentale, à laquelle on donne aussi le nom de musique européenne;

2° La musique orientale.

Les pays dans lesquels la musique orientale est en usage ne sont pas moins vastes que ceux où la musique occidentale est pratiquée. Cependant, la musique occidentale est tellement répandue partout que, même dans les pays où l'on cultiva le plus la musique orientale, on trouve des amateurs qui s'occupent en même temps de la musique dite européenne. Au contraire, dans les principales ville de l'Europe qui sont considérées comme les centres importants de la musique occidentale, les personnes qui s'occupent de musique orientale sont très rares.

La musique moderne est enseignée chez les diverses nations qui sont, au courant de la civilisation européenne, sur la même théorie et sur les mêmes bases fondamentales. Quant à la musique orientale, son véritable caractère est à peu près inconnu des Européens.

Il est juste d'excuser les Européens à ce sujet, parce que jusqu'aujourd'hui tout ce qui a été écrit et publié en Europe sur cette musique est autre chose que le résultat de leurs propres études. Un Oriental n'a pas expliqué aux Européens la musique de son pays dans une langue compréhensible pour les musiciens de l'Europe. Par contre, nous les Orientaux, nous sentons très bien la difficulté qu'un Occidental rencontrera, en s'aidant seulement, des traités théoriques, pour avoir une idée juste du caractère pratique d'une musique telle que la musique orientale, parce que celle-ci est basée sur des principes autres. que ceux de la musique occidentale.

Les traités théoriques de la musique orientale qui sont étudiés par les Européens sont des ouvrages écrits, il y a plusieurs siècles, par divers auteurs dont les idées ne concordent plus avec les idées modernes. Même en Orient, on trouve très rarement un homme qui ait étudié ces ouvrages. Cependant, l'étude sérieuse de ces anciens traités par ceux des musiciens de l'Orient qui sont aussi au courant de la musique occidentale, expliquerait mieux, de quelle manière et d'après quelle théorie la musique occidentale est cultivée depuis longtemps, et le véritable caractère de la musique orientale, très mal connue jusqu'à présent par les Européens serait compris facilement. Cette réciprocité d'études serait profitable pour l'une comme pour l'autre.

D'après nos renseignements, parmi les Européens qui les premiers ont saisi l'intérêt qu'il y a dans la pénétration réciproque de deux musiques, il faut citer Bourgault-Ducoudray. Malheureusement, les vœux émis à ce sujet par cet éminent professeur sont restés lettre morte et n'ont été suivis d'aucun résultat et d'aucune application pratique.

Cependant, comme, on a donné à Bourgault-Ducoudray, lorsqu'il, se trouvait à Constantinople, des idées extrêmement fausses sur la théorie de la musique orientale et sur celle des divers modes de cette musique, comme le distingué professeur a eu, paraît-il, beaucoup de difficultés rétablir une concordance entre les renseignements qu'il a obtenus lui-même des chanteurs de l'Orient et les principes qui se trouvent dans les anciens traités grecs sur la théorie de la musique, il en est résulté de sa part plusieurs hypothèses qui sont loin de la vérité.

Si on lit attentivement les pages où Bourgault-Ducoudray énumère les mesures qu'il juge nécessaires pour réformer la musique orientale, on sent que la question d'établir un trait d'union entre les musiques orientale et occidentale a occupé beaucoup son esprit. Cependant, en Orient, les idées qui régnent sur la théorie de la musique sont tellement contradictoires, qu'il n'est pas exagéré de dire que chaque professeur de musique a sa propre théorie! Les Néo-Grecs, surtout, veulent faire reposer la musique de leurs églises sur des principes théoriques tout à fait curieux, principes qui n'ont aucune valeur scientifique et qui restent les inventions chimériques de certains théoriciens.

Bourgault-Ducoudray doit certainement être excusé de n'avoir pas eu le moindre doute sur l'authenticité des renseignements qu'il a recueillis, puisqu'il les puisait aux sources mêmes, auprès des chantres grecs ; il a donné à ces renseignements une importance qu'ils ne méritaient pas, et c'est sur ces renseignements qu'il a bâti ses observations. Aussi, quoique ses déclarations soient erronées à plusieurs points de vue, son idée est très juste lorsqu'il dit que si la musique orientale était étudiée par les musiciens occidentaux, la musique européenne, « épuisée » par l'emploi excessif des deux seuls modes « majeur » et « mineur », en profiterait beaucoup et que cette étude ouvrirait de nouveaux horizons aux compositeurs européens.

On sait que Bourgault-Ducoudray ne s'est pas contenté, dans son ouvrage susdit, d'émettre ce vœu ; il a voulu aussi faire entendre aux musiciens les divers effets qu'on pourrait tirer de l'emploi, dans la musique moderne, des modes de l'ancienne musique grecque, et de leur application aux ressources immenses de la polyphonie. Dans ce but, il a donné au palais du Trocadéro, le 7 septembre 1878, une conférence dont le compte rendu sténographique a été publié.

Cependant, il est vraiment regrettable que cette idée n'ait pas attiré comme il le fallait l'attention des musiciens de l'Europe. L'immortel Gounod, qui présidait la conférence en question, s'est contenté de dire aux assistants :

« Mesdames, messieurs, au nom du bureau que j'ai l'honneur de présider aujourd'hui devant vous, et en votre nom aussi, je tiens à remercier ces dames et ces messieurs qui ont bien voulu prêter à M. Bourgault-Ducoudray le concours de leur talent et de leur bonne volonté afin de nous faire entendre ces chants qui viennent de nous charmer tous. »

Voilà tout ce qu'a dit Gounod à la fin de cette conférence. N'aurait-il pas dû ajouter quelques mots énonçant ses idées personnelles sur la question proposée? et ses paroles pouvaient-elles blesser « l'officiel Conservatoire de Paris » qui ne connaît que deux modes, majeur et mineur? Je ne sais trop ; mais on voit que Gounod n'est pas assez content de ce que le conférencier le cite, en passant, comme ayant employé dans un de ses opéras l'un des anciens modes grecs. En effet, Bourgault-Ducoudray, au cours de sa conférence, aurait dit ceci :

« Enfin, M. C. Gounod, qui a bien voulu présider cette séance, s'est servi du mode hypodorien au commencement de la romance du Roi de Thulé, dans son opéra de Faust :

Il était un roi de Thulé etc.

(Double salve d'applaudissements.)

« Ces applaudissements, mesdames et messieurs, sont un juste hommage rendu à un homme dont nous sommes fiers. (Nouveaux applaudissements.) Ils prouvent, en outre, que vous ne désapprouvez pas M. Gounod d'avoir fait emploi des modes grecs dans ses ouvrages. M. Gounod me pardonnera de l'avoir cité, je prends mes exemples où je les trouve, et je ne saurais d'ailleurs mieux les choisir que dans ses œuvres. »

Quoi qu'il en soit, la réponse de Gounod peut montrer clairement son état d'esprit.

Naguère, le distingué directeur de la Revue musicale, Jules Combarieu, dans ses cours du Collège de France, a émis de nouveaux vœux (3) pour la réalisation des idées de Bourgault-Ducoudray ; mais je ne sais encore si ces voeux exerceront l'effet désiré sur les compositeurs contemporains.

En effet, le célèbre compositeur Camille Saint-Saëns a voulu reproduire, dans certaines de ses œuvres, les rythmes et les modes de l'Orient, et pour cela il est considéré en Europe comme le fondateur de l'orientalisme en musique; toutefois, son essai est en tout cas élémentaire, et consiste dans une imitation qui semble trop superficielle aux yeux des Orientaux.

D'ailleurs, il faut avouer qu'il n'était pas facile, pour les compositeurs européens, d'emprunter certains éléments de la musique orientale. Jusqu'à ces dernières années, le despotisme qui régnait en Turquie rendait impossible aux Turcs toute manifestation scientifique et artistique aussi bien dans leur pays qu'à l'étranger.

Quoique la Turquie fût le pays où la musique orientale était le plus avancée et le plus cultivée, ni en Turquie, ni en Egypte, ni en d'autres pays de l'Orient on ne rencontrait beaucoup de personnes s'occupant sérieusement de cette musique. Dans cet état de choses, qui pouvait conduire les Occidentaux à saisir le vrai caractère de cette musique? Le moyen unique était donc réduit à ceci : imiter certaines mélodies populaires de l'Orient, entendues par hasard par les compositeurs qui voyagent très souvent en Orient, comme Saint-Saëns, par exemple. Cependant, si on pense que les mélodies qu'on imite n'ont aucune valeur scientifique, on peut concevoir quel crédit auront auprès des musiciens sérieux de l'Orient les œuvres dans lesquelles on introduit ces imitations.

Pourtant, il est bon de remarquer que cette innovation en musique, malgré toute sa défectuosité, n'a pas manqué d'attirer l'attention des Occidentaux. On peut donc juger que si la musique orientale était prise un peu plus sérieusement en considération par les compositeurs de l'Europe, le public européen ne resterait pas aussi insensible à ce mouvement de réorganisation qu'on peut le croire au premier abord.

1. Cf. Etudes sur la musique ecclésiastique grecque, chapitre V, intitulé : De la réforme musicale en Orient, pages 64-76. Paris, 1877.

2. Cf. Conférence sur la modalité dans la musique grecque. Paris, Imprimerie Nationale, 1879.

3. Cf. Revue musicale, n° 10, 11, 12, 13, 14, 15, 16, 17, 18. Paris 1906.

[2947]

Pour arriver à ce but, il fallait expliquer aux Occidentaux la musique orientale telle qu'elle est, c'est-à-dire exempte de toute hypothèse chimérique. Je désirais depuis longtemps accomplir cette tâche difficile, parce que, selon moi, dans le siècle de progrès où nous vivons, il n'est utile pour aucun des deux intéressés que l'Orient et l'Occident restent étrangers l'un à l'autre en fait de musique ; au contraire, par une pénétration réciproque, les Orientaux profiteront beaucoup de l'Occident, et le profit que les Occidentaux retireront de l'Orient ne sera pas moindre.

C'est cette tâche que j'entreprends ici, dans l'espoir de montrer que la musique orientale et la musique turque, en particulier, qui en est un chapitre intéressant, ne méritaient pas la défaveur dont elles sont entourées, surtout parce que leur constitution théorique est très logique.

II  Quelle faut-il entendre lorsqu'on dit « la musique orientale » ?

Il résulte de ce qui précède que la musique des diverses nations de l'Orient et les musiques qu'on entend dans les autres pays où la musique moderne, dite occidentale, n'est pas répandue, sont des musiques auxquelles on donne le nom général de musique orientale. Ici, il faut un peu expliquer ce que nous voulons dire.

Les musicologues européens qui parlent de la musique des nations orientales ont émis sur ce sujet des idées et des appréciations très curieuses. Entre autres, s'il faut s'en rapporter aux déclarations données par Fétis, dans son Histoire générale de la musique, sur l'histoire de cet art chez les Arabes, Turcs et Persans, il serait nécessaire d'admettre qu'il existe des différences essentielles entre la musique arabe et la musique turco-persane. S'il est vrai qu'aujourd'hui nulle « différence de théorie » ne distingue ces diverses musiques, il n'en est pas moins vrai que, jadis, les différences secondaires d'exécution et de style propres à chaque nation n'existaient pas encore, en raison du faible degré d'avancement de l'art musical ; mais actuellement on peut facilement distinguer une chanson arabe d'une chanson turque.

Il faut faire attention cependant à ce que cette possibilité de discrimination ne résulte pas, comme Fétis et tant d'autres le pensent, de ce que les Arabes divisent l'octave en dix-sept intervalles, et les Turcs et Persans en vingt-quatre intervalles ; mais uniquement de ce qu'il y a différence de « style », de « manière de chanter », tandis que les tons qui entrent dans la composition des chants de ces mêmes nations restent les mômes.

Ici on peut m'objecter ceci : on voit dans les pays d'Orient un Arabe ou un Turc prendre, par exemple, une mandoline fabriquée en Europe et dont le manche contient des touches fixes d'après le tempérament égal qui divise l'octave en 12 demi-tons, et jouer pourtant sur cet instrument les mélodies de sa propre musique. Si l'octave est divisée en 24 intervalles, comment cet Oriental est-il satisfait en jouant une telle mélodie sur une mandoline? On peut répondre à cette objection comme il suit : « Moi aussi j'entends chaque jour ces mélodies orientales jouées sur une mandoline ou sur un piano. Pour vous donner une idée de l'impression que ces mélodies donnent aux Orientaux dont les oreilles sont habituées à n'entendre que de purs intervalles mélodiques, je vous ferai la comparaison suivante : par exemple, il y a, en français cinq voyelles et deux diphtongues : a, e, t, o, u, ou, eu, ce qui fait sept sonorités distinctes ; mais les Italiens, d'origine latine comme les Français, n'ont jamais songé à utiliser les sons u ni eu, que leurs lèvres pourraient prononcer aussi bien que celles des Français, et ils s'en tiennent, sauf dans certains dialectes, aux cinq sons : a, e, i, o, ou (ce dernier s'écrivant u). Il en est de même en musique : dans la musique orientale, il y a deux si bémol entre la et si naturels. Si nous appliquons notre exemple sur la corde du la d'un violon dont la longueur est de 333 millimètres, nous aurons une idée précise de la position de ces deux si bémols :

 

« Dans le chant des peuples orientaux, il y a des modes dans lesquels après la q, par exemple, ou n'importe quelle autre note naturelle, on hausse la voix dans la mesure d'un intervalle nommé lima (243/256) et il y a aussi des modes dans lesquels après la bq, la voix est haussée d'un intervalle nommé apotome (2048/2187).

« Or, en jouant ces modes sur un piano, que fait un Oriental ? Il se voit obligé certainement d'employer l'unique si-b au lieu du 1er et du 2e si-b. Dans ce cas, le caractère mélodique de chaque mode est faussé très sensiblement et ce fait est très semblable, d'après la comparaison précédente, à la prononciation d'un mot de la langue française d'après la prononciation italienne, c'est-à-dire à la prononciation du mot musique comme mousique ; la souffrance que ressent un Oriental en entendant un si b de sa musique remplacé par un si b de la gamme fausse dite tempérée, est la même que celle de l'oreille d'un Français entendant le mot musique prononcé mousique. »

1. Par le terme « différence de théorie » j'entends le système tonal de chaque nation, c'est-à-dire la théorie mathématique de sa gamme fondamentale, des nombres et des valeurs des tons naturels et des tons intermédiaires qui entrent dans la composition des modes lorsque ces peuples les chantent.

2. J'emprunte cette comparaison à l'excellent ouvrage de M. Albert Lavignac. Cf. la Musique et les Musiciens, page 420. Paris, 1805.

[2948]

Mais revenons à notre sujet. Nous parlions des déclarations de Fétis concernant la musique des Orientaux. En effet, Fétis, pour pouvoir démontrer une différence de théorie entre la musique arabe et la musique turco-persane, a émis tant d'hypothèses dans son histoire générale de la musique, que si on veut les réfuter ligne par ligne, il faudrait écrire des pages qui formeraient cinq volumes comme son histoire. Nous nous en tiendrons aux critiques essentielles.

La vérité, c'est que la division de l'octave est strictement la même chez les Arabes, chez les Turcs, chez les Persan» et, en un mot, partout où on entend la musique orientale, la divergence de théorie qu'on voit chez certains auteurs anciens ou modernes provient de leur manque de clairvoyance dans l'étude des diverses questions qui demandent une connaissance approfondie et poussée à un égal de degré de la musique à la fois théorique et pratique.

Les hypothèses de Fétis sont tellement curieuses que nous ne pouvons pas nous dispenser de faire une seconde comparaison à ce sujet : si un homme prétendait aujourd'hui que la différence de style et d'école entre les musiques française, allemande et italienne provient de la manière dont l'octave est divisé chez chacune de ces trois nations et que, par exemple, le mi des Allemands est plus grave que le mi des Français et des Italiens, le la du diapason normal étant le même, comment les musiciens de l'Europe accueilleraient-ils une telle assertion ? Les déclarations de Fétis à ce sujet produisent le même effet chez les musiciens orientaux éclairés.

On ne peut pas nier que la chose qui attire tout d'abord l'attention d'un musicien européen, lorsqu'il commence à étudier la musique orientale, c'est la composition de l'octave par des intervalles divisés autrement qu'en Europe. Les Occidentaux qui ont lu dans les ouvrages théoriques des musiciens arabes que l'octave est divisée en dix-sept intervalles, ont pensé que le ton est divisé chez les Arabes en trois parties égales, et, par conséquent, que la musique, arabe emploie des tiers de ton. Sous la domination de cette idée mal conçue, ils s'empressèrent en 1867, à l'Exposition de Paris, où des musiciens tunisiens donnaient des concerts, de rechercher comment la voix humaine peut diviser le ton en trois parties égales. Cela démontre que, dans ce temps-là, on croyait en Europe que dans la musique arabe ces tiers de ton étaient employés l'un après l'autre !

Les musiciens occidentaux qui ont entendu les chanteurs tunisiens, tout en ne pouvant juger définitivement qu'il y a des tiers de ton dans leurs chants, n'ont pas mesuré la véritable valeur de certains intervalles musicaux qui paraissaient étranges à leurs oreilles, et ont conclu que la théorie du tiers de ton n'était pas tout à fait sans fondement.

Fétis, dans le deuxième tome de son Histoire générale de la musique, publiée en 1869, c'est-à-dire deux ans après cette exposition, a de nouveau bouleversé la question. D'après ses allégations, la musique arabe contiendrait des tiers de ton.

« Le système vrai de cette, musique, dit-il, a pour base l'égalité des tons conformes aux principes des pythagoriciens, dans la proportion de 9:8, et les demi-tons mineurs, comme les limma, c'est-à-dire dans la proportion de 256:243. Or ces tons majeurs sont divisés par tiers, dans la théorie de la musique arabe, au lieu de l'être par deux demi-tons, l'un mineur (256/243), l'autre majeur (2187/2048). »

Selon cette assertion, la gamme fondamentale de la musique arabe serait la même que la gamme dite pythagoricienne ou ditomique et dont les rapports sont les suivants :

 

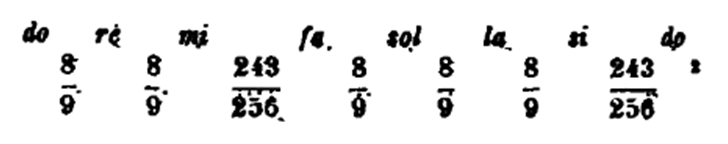
Quant aux tiers de ton, ils se trouveraient, d'après le désir de Fétis, entre chaque ton majeur, en le divisant en trois parties égales ! …

Cependant, à aucune époque, aucun théoricien arabe n'a considéré la gamme ditonique susdite comme la vraie gamme de la musique arabe, et aucun auteur n'a parlé de la division du ton majeur en trois parties égales. De même, aucun théoricien turc ni persan n'a émis une idée si singulière.

Au contraire, tous les théoriciens orientaux parlent d'une seule gamme comme base du système oriental ; dans cette gamme, les tons sont de dix sortes, l'un majeur (8/9) l'autre mineur (9/10), et les demi-tons majeurs (15/16).

En outre, si, dans la gamme fondamentale de l'Orient, le 1er demi-ton se place entre les 3e et 4e notes, — comme dans la gamme majeure de la musique moderne, - le 2e demi-ton n'est pas entre les 7e et 8e notes, mais au contraire se trouve placé entre les 6e et 7e notes de la gamme. Dans ce cas, la gamme fondamentale de l'Orient nous apparaît sous la forme suivante :

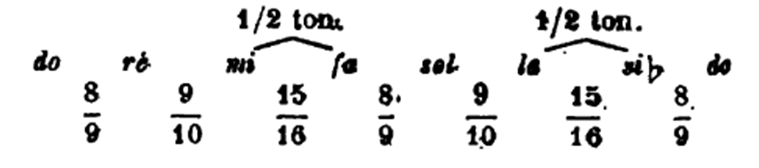
Si nous faisons attention, nous verrons que cette gamme n'est autre chose que la gamme de Gui d'Arezzo qui commence par sol :

 

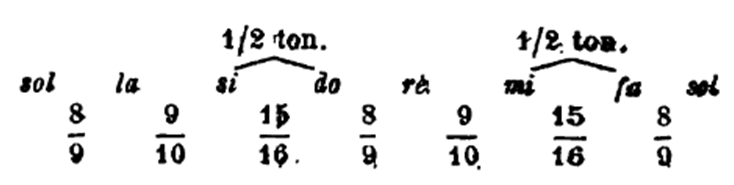
D'ailleurs, il résulte des études historiques qu'aussi chez les anciens Grecs, l'ensemble des sons employés qui portait le nom de système parfait et qui était composé de deux octaves, était arrangé de la manière susdite. Cet arrangement du système parfait se nommait système séparé grave.

Si nous faisons une comparaison entre la gamme adoptée par les théoriciens orientaux — qui est identique à celle de Gui d'Arezzo — et la gamme de la musique moderne, nous voyons que la gamme orientale est formée de l'adjonction immédiate de deux tétracordes semblables, et de plus d'un ton majeur du côté aigu; cette forme de l'octave porte le nom de système conjoint :

 

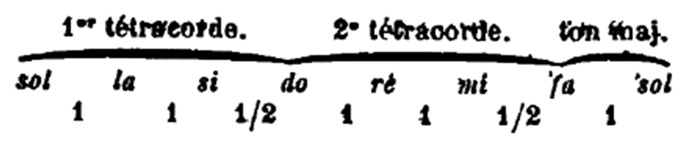
La gamme type des Occidentaux est d'une autre constitution; elle est composée de deux tétracordes disjoints par un ton, identiques l'un à l'autre dans la disposition de leurs intervalles :

 

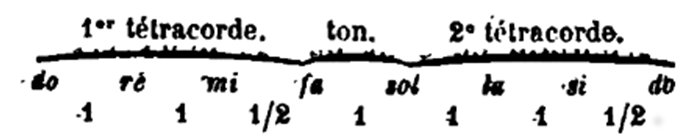
[2949]

Le célèbre théoricien turc Farabi (xe siècle), qui a étudié longuement les ouvrages musicaux des Grecs, a adopté cette gamme « système séparé grave » ou « système conjoint » comme gamme fondamentale de la musique orientale. De même, cette gamme est celle des Turcs et des Persans. La gamme orientale une fois ainsi déterminée, il s'agissait d'une autre question. Par quelle note de la musique moderne faut-il la faire commencer, d'après l'état actuel des instruments occidentaux et orientaux ? Cette question a occupé et occupe encore l'opinion des musiciens de l'Orient. Fétis l'a même abordée, et a dit que les théoriciens de la musique turque prennent sol pour point de départ de la gamme (1). Les Orientaux pensent qu'il n'est pas convenable de faire commencer leur gamme au do, comme les Européens, ou au sol, comme Fétis le déclare. A ces deux cas ils trouvent des inconvénients. Pour le moment, disons que les intervalles de la gamme fondamentale de la musique orientale sont disposés dans l'ordre suivant :  

8/9+9/10+15/16+8/9+9/10+15/16+8/9

Nous étudierons plus tard la question de savoir s'il faut prendre pour point de départ l'une des notes do ou sol, ou bien jr, pour l'adaptation d'une gamme ainsi disposée. Les détails précédents ont fait voir que la gamme fondamentale de l'Orient contient (rots sortes d'intervalles : 

1° Le ton majeur, qui est représenté par 8/9, 

2° Le ton mineur, qui est représenté par 9/10 ; cependant.je répète que ce 9/10 est la valeur approximative du ton mineur employé dans la musique orientale. La valeur juste en est 59049/65536 , parce que le ton mineur de la musique orientale est composé de deux limma. Par conséquent : 

243/256x 243/256=59049/65536

3° Le demi-ton majeur qui est représente par 15/16 ; cependant, ce 15/16 est lui aussi la valeur approximative du demi-ton majeur. La valeur juste en est  2048/2187, et on lui donne le nom d'apotome. 

Dans ce cas, la gamme fondamentale de la musique orientale est composée des intervalles dont les valeurs justes sont les suivantes : 

On sait qu'aucune musique ne se compose exclusivement des notes naturelles; au contraire, entre ces notes, dites naturelles d'après les règles de la notation musicale, on intercale d'autres notes plus petites, et à chacune de ces notes on donne dans la musique européenne le nom de demi-ton. Cependant, d'après l'exigence du tempérament qui est usité dans la musique moderne, la gamme dite naturelle n'étant composée que de deux sortes d'intervalles, c'est-à-dire du ton et du demi-ton, il n'y avait pas lieu de diviser de nouveau les demi-tons en deux, et il se trouve entre les tons un seul demi-ton. Pourtant, même les violonistes européens doués d'une oreille sensible et d'un haut sentiment musical, lorsqu'ils ne jouent pas en accompagnant un instrument à touches fixes comme le piano, n'emploient pas un seul demi-ton entre les notes naturelles, mais ils conservent toujours une différence sensible d'intonation, par exemple, entre un do # et un ré b ; ils font les do # un comma plus aigu que les ré b. 

1. Cf. Histoire générale de la musique, tome II, page 363. Pourtant, les déclarations de Fétis dans cette page sont erronées, puisqu'il dit qu'il y a de sol à la 9 commas; de la à si #, 7 commas; de si à ut, 7 commas. Il n'est pas juste de dire pour les intervalles la-si #. si #-ut, qu'ils sont composés de 7 commas chacun, puisque l'intervalle (la-si #) est dans la valeur de 9/10, et l'intervalle (si-ut) est dans la vais leur de 15/16 ; cela signifie que le premier est plus grand que le second. 

 2. Je tiens à rappeler que, au cours de mon étude, les fractions ordinaires qu'on rencontrera et dont le dénominateur est plus grand que le numérateur, désignent des rapports de longueurs des cordes; par exemple, si nous disons qu'entre sol et la il y a la valeur 8/9, cela signifie que sur une corde tendue qui donne à vide le sol et dont la longueur totale est de 900 millimètres, si nous mettons notre doigt, de façon à la raccourcir de 100 millimètres, à partir du sillet, et si nous faisons vibrer les 800 millimètres de cette corde, nous aurons le son de la. Au contraire, si le numérateur est plus grand que le dénominateur, comme dans 9/8, ce rapport désigne le nombre de vibrations c'est-à-dire, en appliquant l'exemple précédent, si on dit qu'entre sol  et la il y a le rapport de 9/8, cela signifie que si sol fait 800 vibrations, la en fait 900. 

3. Nous voulons expliquer ici un point qui est mal interprété jusqu'à présent par les théoriciens européens. Dans les ouvrages musicaux des Européens on parle d'un petit intervalle auquel on donne le nom 524 28R de comma de Pythagore et dont la valeur est représentée par 524288/531441.

Chaque auteur a envisagé la raison d'être de ce comma d'une manière différente. Ecoutons ce que dit de ce comma H. Riemann, pour prendre le plus récent de ces auteurs, dans son Dictionnaire de musique (traduction française, page 153) : « Le comma de Pythagore, dit-il, dont l'intervalle de six tons entiers, dans le rapport 9 : 8, dépasse l'octave 96/86 :2/1» Le même auteur, pour expliquer le comma 81/80, qui est accepté dans la théorie de la musique moderne, dit ceci : « Le comma Didymique ou Syntonique, 80:81, différence du petit ton entier au grand ton entier = 9/8 : 10/9 . » Par conséquent, pour expliquer le comma de Pythagore, au lieu d'imaginer la succession de six tons majeurs et de l'adjonction d'un petit intervalle afin que le total de ces six tons mineurs devienne l’octave, il vaudrait mieux dire ceci, conformément à la réalité : Le comma de Pythagore est, dans la théorie de la musique ancienne grecque et dans celle de la musique orientale en général, la différence qu'il y a entre le ton majeur et le ton mineur. En effet, le comma de Pythagore n'est autre chose que la différence du ton majeur (8/9) et du ton mineur (59049/65536)

59049/65536x524288/531441=8/9

[2050]

Et maintenant, dans la musique orientale combien se trouve-t-il de tons intermédiaires (pour ne pas dire demi-tons) entre les notes de la gamme fondamentale ? et ces tons intermédiaires, d'après quelle règle sont-ils répartis? Pour obtenir la réponse, il faut jeter un coup d'œil sur les trois espèces d'intervalles de la gamme en question. 

1° Ton majeur (8/9). Chacune des deux notes de la gamme entre lesquelles se trouve l’intervalle du ton majeur contient trois notes intermédiaires qui sont représentées, dans la notation, tantôt comme le bé-mol de la note naturelle qui se trouve à l'aigu, et tantôt comme le dièse de la note naturelle qui se trouve au grave. Par exemple, prenons les deux notes sol et la dont l'intervalle est, dans la musique orientale, égal à 8/9. Si nous partons de sol vers le côté aigu, nous avons d'abord un sol # avec la valeur de243/256 ; puis, nous avons un second sol # avec la valeur de 2048/2187 (toujours à partir de sol #); et enfin nous avons un troisième sol # avec la valeur de 59049/65536, mais qui est toujours représenté dans la notation, non pas comme un sol #, mais comme un lab (1) Par conséquent, le ton majeur de la musique orientale est divisé ainsi : 

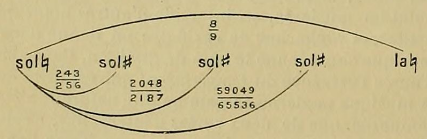
2° Ton mineur (59049/65536). Chaque groupe de deux notes qui ont entre elles cet intervalle du ton mineur contient deux notes intermédiaires. Prenons comme exemple les notes la et si. Si nous partons du la vers le côté aigu, nous avons d'abord un lait avec la valeur de 243 /256, et puis nous avons un second la # avec la valeur 2048/2187. Le ton mineur est donc divise ainsi : 

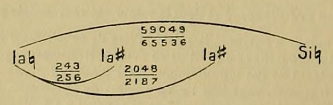
3° Demi-ton majeur (2048/2187). Deux notes qui ont entre elles cet intervalle de demi-ton majeur contiennent aussi deux noies intermédiaires. Prenons comme exemple les notes si et do. Si nous partons du si vers l'aigu, nous avons un si 'J avec la valeur de 524288/531441 ; et puis, en allant toujours à l’aigu, nous avons un si # avec la valeur de 243/256, mais qui est aussi représenté dans la notation, non pas comme un si #, mais comme un do b. Le demi-ton majeur se divise alors ainsi : 

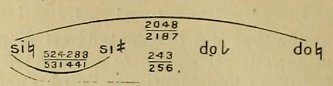
Nous arrivons donc à ce résultat que les intervalles qui constituent la gamme fondamentale de la musique orientale ne sont pas de deux espèces, l'un ton et l'autre demi-ton, comme cela se passe dans la pratique de la musique moderne, mais que ces intervalles sont, en théorie aussi bien qu'en pratique, de trois espèces. \in outre, les notes naturelles de cette gamme orientale ne sont pas réparties comme celles de la gamme occidentale, et il y a entre les tons majeurs ( 8/9) « trois », entre les tons mineurs (59049/65536) « deux » et entre les demi-tons majeurs (2048/2187) également « deux » notes intermédiaires. 

Les instrumentistes orientaux, qui s'occupent seulement de la pratique de leur musique, voyant que l'intervalle de ton majeur comprend trois notes et que, en fait, le ton majeur est divisé en quatre parties, ont donné le nom de quart de ton à chacune de ces quatre parties. Et les Européens qui ont entendu ce terme ont conclu que les Orientaux divisent le (ou en quatre parties égales, tandis qu'à aucune époque nul théoricien, qu'il fût Arabe, Turc ou Persan, n'a parlé de la division du ton majeur en quatre parties égales. Notre précédent exemple montre, au contraire, que dans l'intervalle de sol-la à partir de sol, on a pris : 

1° 243/256, 2° 2048/2187, et 3° 59049/65536 ;  les intervalles ainsi obtenus ne divisent certes pas le ton majeur en quatre parties égales. Nous pouvons dire maintenant que la musique orientale est une musique qui a une gamme fondamentale dont les notes naturelles et leur position, ainsi que les notes intermédiaires, sont autrement disposées, quelquefois en qualité et quelquefois en nombre, que dans la musique occidentale et qu'elle possède, en dehors des deux modes majeur et mineur des Européens, plusieurs modes très doux et très caractéristiques, produits par la combinaison de ces divers intervalles mélodiques. 

Quelles sont les contrées où cette musique dite orientale est répandue? 

Pour préciser, nous citerons les pays suivants : Turquie d'Europe, Turquie d'Asie, Arabie, Egypte, Palestine, Syrie, Crète, Chypre, les îles de l'Archipel, Epire, Thessalie, Péloponèse, Tripoli de Barbarie, Tunisie, Algérie, Maroc, Perse, Inde, Turkestan, Afghanistan... et probablement la Chine et le Japon. Si un musicologue tout à fait au courant de la théorie et de la pratique de la musique orientale fait un voyage dans ces pays, — abstraction faite des divergences de style et d'expression résultant de la diversité des langues, — il verra que les peuples qui habitent les contrées énumérées ci-dessus, tout en étant privés des premières notions de la musique, chantent des mélodies;

1. Ce demi-bémol s'emploie pour désigner que la note qu'il précède est diminuée d'un comma de Pythagore. 

2. Ce demi-dièse fait hausser la note qu’il précède dans la valeur d'un comma de Pythagore. 

[2951] 

si ces mélodies sont analysées, il aura la conviction qu'elles sont basées sur une gamme fondamentale dont la constitution est expliquée plus haut, et que ces mélodies sont composées dans les divers modes dans la composition desquels entrent les tons intermédiaires sus-énoncés. D'ailleurs, il ne saurait en être autrement, puisque les anciens théoriciens orientaux disent formellement que la théorie de la musique est tirée de l'étude des chants des hommes doués par la nature de l'instinct musical, de même que la grammaire d'une langue est construite après que cette langue s'est préalablement formée. Pour justifier notre thèse, supposons que notre musicologue en voyageait entendu la chanson populaire qui suit :

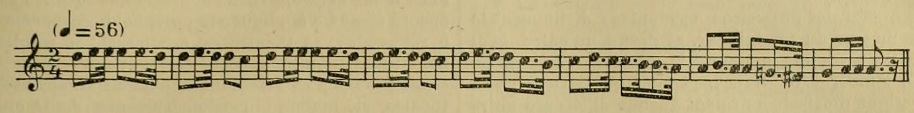
C'est une simple mélodie populaire recueillie en Asie Mineure, parmi les paysans de la province d'Adana. Son auteur n'est pas connu, et même, s'il était connu, on apprendrait que c'est un paysan n'ayant reçu aucune éducation musicale, orientale ou occidentale. Ce qui nous importe, c'est d'ailleurs, non pas le compositeur, mais le mode dans lequel elle est composée. Si nous montrons cette mélodie telle qu'elle est écrite à un Européen, et si nous lui demandons la tonalité de cette mélodie, il nous dira que c'est le « ton de la mineur sans note sensible! ». Elle n'est cependant pas du ton mineur. Entre le mode auquel cette mélodie appartient et le mode mineur il y a une si grande différence qu'en Orient, même un homme qui ne sait pas la musique peut facilement distinguer cette mélodie d'une autre écrite vraiment dans le ton de la mineur'. Pour qu'on puisse faire une comparaison, écrivons une mélodie turque qui est essentiellement composée dans le ton de la mineur :

Si nous ne mettons pas dans cette mélodie, avant les notes si, le demi-dièse ainsi noté # comme négligent de le faire les musiciens turcs eux-mêmes, pour un musicien occidental qui comparera ces deux mélodies, la différence se réduira dans la première mélodie à ces deux points : 1° La note sensible manque; 2° La sur-dominante fa est diésée. Un musicien européen, étant habitué à employer un sic, invariable, ne songe nullement que les si de ces deux mélodies soient différents l'un de l'autre, et dit sans hésiter que la première mélodie est dans le ton de la mineur sans note sensible. Au point de vue de la musique orientale, ces deux mélodies sont de deux modes qui sont tout à fait distincts l'un de l'autre : La base de la 1e mélodie est le tétracorde (la-ré), plus la note mi ajoutée à l'aigu et les notes sol et fa ajoutées au grave, pour orner la mélodie. Le tétracorde de cette mélodie est composé à partir du la? .

1° d'un ton mineur; 2° d'un demi-ton majeur; 3° d'un ton majeur : Tétracorde. 

La base de la 2° mélodie est, non pas un tétracorde, mais un pentacorde, plus les notes faq et sol ajoutées à l'aigu, et sol^ ajoutée au grave pour l'ornement de la mélodie. Ce pentacorde se compose à partir du la: l" d'un ton majeur; 2° d'un limma; 3° d'un ton majeur; 4° également d'un ton majeur : 

 

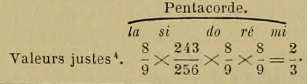
1. Le ton de la mineur est très employé en Orient. Les Turcs lui donnent le nom île mode Poucelik. 

2. Les théoriciens occidentaux disent que la différence entre le ton majeur et le ton mineur est négligeable. Cependant la musique orientale accorde beaucoup d'importance au respect de cette différence, et les détails suivants montreront que cela n’est pas sans raison. Pour donner au lecteur une idée pratique de cette différence soi-disant négligeable, faisons un essai, en jouant ces deux mélodies sur le violon. Vu que la partie sonore des cordes du violon est ordinairement de 333 millimètres de longueur, et que les si de la première mélodie se trouvant dans l'intervalle de 59049/65536 à partir du la, il faut que nous mettions notre doigt sur la corde libre la, à partir du chevalet, juste  à 300 millimètres. Tandis que dans la deuxième mélodie les si# étant éloignés du la dans la valeur d'un ton majeur 8/9, pour trouver les si ; de cette mélodie, il faudrait mettre notre doigt sur le 296e millimètre de longueur de la corde à partir du chevalet. Il n'est pas nécessaire d'expliquer ici ce qu'un espace de plus de 4 millimètres peut engendrer de différence d'intonation sur un instrument sensible comme le violon. Je crois qu'avec cet exemple on comprend facilement pourquoi la différence du ton majeur au ton mineur n'est pas négligeable dans la musique orientale. Supposons que ces mélodies soient jouées par un violoniste européen ; celui-ci étant habitué à jouer son instrument en tempérant les intervalles et étant obligé de faire vibrer le 890899/1000000  corde la pour réaliser si # de la gamme tempérée, mettra son doigt sur le point 296 669367/1000000 . L'oreille d'un musicien oriental ne pourra sentir la petite différence lorsque le violoniste jouera la 2e mélodie; mais quant à la 1e mélodie, le si du violoniste européen lui paraîtra tellement aigu qu'il conclura à la fausseté du jeu du violoniste. 

3. Dans un intervalle de quarte, en d'autres termes dans un tétracorde, il y a plusieurs façons de disposer des intervalles mélodiques. Nous le verrons plus tard. 

4. Les intervalles du ton majeur et du limma n'ont que leurs valeurs justes. 

[2952] La différence la plus essentielle et la plus caractéristique qui divise les deux musiques orientale et occidentale, c'est l'existence et l'emploi en pratique de ces intervalles mélodiques dans la première, et, dans la seconde, l'absence totale de leur emploi en pratique, bien que les physiciens en aient reconnu l'existence, ainsi que l'ignorance officielle d'autres modes en dehors du mode majeur et du mode mineur. En effet, les physiciens occidentaux distinguent le ton majeur du ton mineur, et disent qu'entre do et ré il y a un ton majeur 8/9, et entre ré et mi un ton mineur 9/10. Mais les traités qui parlent de la pratique musicale ne voient aucune différence entre do-ré et ré-mi. De même, les demi-tons sont considérés comme s'ils divisaient le ton en deux parties égales, et on n'attache aucune importance à distinguer le limma (243/256) de l’apotome (2048/2187), qui sont les véritables valeurs du demi-ton mineur et du demi-ton majeur même dans la musique européenne. Les physiciens occidentaux ont eu tort de rejeter ces valeurs rationnelles pour les remplacer par des valeurs irrationnelles comme 24/25 au lieu de 243/256, et 25/27 au lieu de 2048/2187.

 Il est bon de remarquer que cette faute des physiciens occidentaux avait attiré l'attention d'un simple accordeur de pianos nommé C. Montai. En effet, en parlant (1) de la différence qui existe entre la théorie et la pratique de la musique moderne, ce praticien dit justement : « Si les physiciens avaient donné au dièse le rapport de l’apotome 2187/2048 au lieu du rapport 25/24, la théorie aurait été d'accord avec la pratique, et le ton se serait divisé en deux demi-tons correspondant à l’apotome et au limma, qui sont précisément égaux, à très peu de chose prés, aux demi-tons chromatique et diatonique pratiqués (2). » Ces paroles, malgré leur exactitude, sont restées malheureusement sans écho chez les physiciens, puisque ceux-ci n'ont rien changé, depuis, à leur ancienne théorie des dièses et des bémols. Je ne comprends pas à quoi sert une théorie imaginée au cabinet et qui n'est pas conforme à la pratique des musiciens! 

Voilà pourquoi lorsqu'un Oriental, dont l'oreille est habituée depuis son enfance à entendre les purs et justes intervalles mélodiques, entend une mélodie orientale jouée sur le piano, son oreille n'est nullement satisfaite des sons tempérés du piano et trouve cette mélodie sensiblement dénaturée. Si vous lui demandez quelles sont les notes qui blessent son oreille, il ne pourra donner une réponse précise, même s'il est musicien, et il a raison, parce que, par suite du tempérament égal, chaque note a changé, plus ou moins, sa place véritable. 

Par conséquent, de même que les musiciens orientaux accueillent la musique jouée sur le piano comme une musique factice pour ainsi dire, les Européens, de leur côté, qui n'ont jamais entendu depuis leur enfance que des intervalles tempérés, disent, lorsqu'ils voyagent en Orient et qu'ils entendent pour la première fois les chants des Orientaux composés de purs intervalles mélodiques, que les Orientaux chantent par tiers ou par quart de ton, pour ne pas dire, par politesse, qu'ils chantent faux! Nous terminerons ici cette discussion. Ce que nous avons voulu faire comprendre, c'est que par musique orientale il faut entendre une musique homophone, mais d'une extrême richesse mélodique, qui n'a pas encore essayé d'appliquer la polyphonie européenne à ses modes; sa théorie est exactement le résultat des études minutieuses des lois qui gouvernent le chant des peuples orientaux depuis des temps assez reculés, et, malgré l'invasion croissante de la musique moderne, elle a pu conserver son existence et son indépendance. La musique des Turcs, des Arabes, des Persans, des Indiens et, d'après toute probabilité, celle des Chinois et des Japonais, constitue, par conséquent, les divers chapitres du grand livre qui porte le titre général de Musique orientale. 

III. Y a-t-il une différence de théorie entre les musiques des divers peuples orientaux? 

La différence de théorie imaginée par certains historiens musicaux et surtout par Fétis, différence qui aurait existé entre les musiques des divers peuples de l'Orient, n'existait pas en réalité à. ce moment, de même qu'elle n'existe pas davantage aujourd'hui. Par conséquent, on ne peut tenir pour vraies les déclarations de Fétis à ce sujet, déclarations qui se trouvent dans le 2e tome de son Histoire générale de la musique. En effet, cet auteur prétendant que les Arabes divisent leur échelle tonale en 17 intervalles, et les Turcs et les Persans en 24 intervalles, veut en déduire ce résultat qu'il y a une différence de théorie entre les peuples d'origine sémitique, comme les Arabes, et entre les peuples aryens et touraniens, comme les Turcs et les Persans! 

Fétis se contredit, parce que, d'après lui (3), — et j'accepte complètement son point de vue à ce sujet, — l'aptitude à diviser l'octave en 24 intervalles s'est manifestée dans la plus haute antiquité chez les Aryas de la Perse. La musique qui est née de cette aptitude, une fois réalisée en Perse, s'est propagée d'un côté vers les Indes et de l'autre côté vers l'Asie Mineure; puis, elle a gagné la Grèce par les Lydiens et les Phrygiens, qui sont les descendants des émigrés de la Perse connus sous le nom de Pélasges. Une fois l'identité du système tonal des anciens Persans et des anciens Grecs ainsi établie, jetons un coup d'œil sur l'histoire de la musique chez les Arabes. Ce coup d'œil nous convainc que les Arabes ont reçu des Persans les premières leçons de chant. Les livres littéraires des Arabes sont pleins de citations qui justifient notre conviction.

Voici, entre autres, un fait précis. D'après les déclarations de Aboul-Faradj-Isphahani, dans son célèbre ouvrage Al-Afghani, un Arabe nommé Said ben Mouçadjidj, se sentant des dispositions pour la musique, partit pour la Perse, au milieu du Ier siècle 

1. Cf. l'Art d'accorder lui-même son piano, page 178. Paris, 1836.

 2. On voit qu'ici. Montai désigne l’apotome et le limma par des rapports inverses de ceux qui ont été indiqués plus haut et qui se fondaient sur la longueur des cordes, tandis que les rapports de Montai donnent le nombre des vibrations, lequel est en raison inverse do la longueur des cordes. (Note de la Direction.) 

3. Cf. Histoire générale de la musique, tome II, pages 357 et 369. 

[2953]

de l'hégire, pour s'y perfectionner dans cet art. Il y étudia, dit Aboul-Faradj, le jeu des instruments de musique et la pratique de la musique persane; à son retour, passant par la Syrie, il étudia aussi la musique des différents peuples syriens. Lorsqu'il revint au Hedjaz, il réforma la musique arabe par de légères suppressions et additions, c'est-!i-dire en adaptant seulement à cette musique ce qui lui avait plu dans le chant des Perses el des Grecs de Syrie, et en renonçant à ce qui n'était pas conforme au goût arabe. Aboul-Faradj, quelques lignes plus loin, parle pour la seconde fois de Saul et dit ceci : « C'est lui qui a chanté le premier parmi les Arabes d'après les règles reçues des Persans. » D'ailleurs, les noms de la plupart des modes de la musique arabe sont des mots persans : cela aussi montre que les Arabes ont fait des emprunts à la musique persane, même en ne changeant pas les noms des modes. Mais il parait aussi que Saïd n'est pas le seul réformateur du chant arabe, parce que Aboul-Faradj cite après Said le nom d'un autre musicien arabe nommé lbn Mouhryz, et il résulte de son témoignage qu'lbn Mouhryz a contribué beaucoup à la propagation du nouveau système de chant implanté en Arabie par Said. D'autre part, un des plus célèbres littérateurs arabes, Ibn-Noubaté, dans un commentaire qu'il a écrit pour le traité de Ibn-Zeydoun (1), parle d'un autre musicien arabe nommé Nadre-ben-Haree-ben-Khildé, qui aurait voyagé en Perse avant la proclamation de l'islamisme par Mahomet, se serait attaché à Chosroès Ier, et aurait appris le jeu de l'oud et le chant persan, puis serait retourné en Arabie pour enseigner à la population de la Mecque l'oud et le chant. On sait que, sous Chosroès Ier, la musique était très florissante en Perse, et que le célèbre chanteur Barbud, qui était à sa cour, avait inventé trente modes (2) dont les noms sont appelés, par les historiens qui parlent du siècle de ce roi,  c'est-à-dire trente modes de Barbud.

Le célèbre historien arabe Ibn-Khaldoun expose aussi, dans le 31e chapitre de la préface de son histoire qui est intitulé de l'art du chant, que les Arabes, durant leurs siècles d'ignorance, avant l'islamisme, avaient une musique tout à fait rudimentaire, et que plus tard, en empruntant plusieurs modes à la musique persane, leur musique se perfectionna sensiblement.

Ici, il faut remarquer que l'emprunt des Arabes aux Persans se réduit seulement au côté pratique de cet art. Ou rencontre dans les histoires arabes des citations ainsi conçues : « Quelques chanteurs persans sont arrivés à la Mecque, et les Arabes commencèrent à imiter leur chant; » ou bien : « Quelques Arabes qui étaient partis pour la Perse, où ils avaient étudié l'art du chant des Persans, apprirent de leur côté le chant persan à leurs concitoyens lorsqu'ils rentrèrent dans leur pays. » Ce sont là toujours des emprunts purement pratiques. Quant au côté théorique, on ne rencontre aucune citation historique constatant qu'avant l'islamisme ou plus tard, pendant le Ier siècle de l'hégire, il se soit trouvé des théoriciens de la musique en Perse, il est vrai que sous Chosroès Ier, comme il est dit plus haut, vivait un chanteur renommé, Barbud ; mais on se contente de le tenir pour un praticien très habile, et on ne dit point qu'il ait écrit un ouvrage théorique sur la musique. De cela, nous pouvons conclure que la musique qui, seulement dans les siècles derniers, a été baptisée orientale, en Europe, est née dès la plus haute antiquité chez les Aryas de la Perse (3) et que, de là, elle s'est répandue dans les siècles suivants chez les principaux peuples; elle a été l'objet, pour la première fois, d'éludés théoriques chez les philosophes grecs comme Pythagore et ses successeurs, et à ce moment seulement elle a pris la forme d'une science; c'est la théorie de cette science musicale (4) qui a été empruntée aux Grecs par les Arabes, ainsi d'ailleurs que d'autres sciences, et en même temps les Arabes reçurent beaucoup des Persans au point de vue pratique de cet art. 

En jetant un coup d'oeil sur l'histoire de la musique chez les Turcs, nous verrons que, soit dans les contrées asiatiques qui sont leur pays d'origine, soit dans l’Asie Mineure où ils ont fait plus tard leur migration, la musique cultivée était basée sur la division de l'octave en 24 intervalles, et par là on comprend que la musique turque ne saurait être que semblable à la musique persane. 

Par conséquent, il est tout à fait inadmissible qu'une différence de théorie existe entre la musique des Turcs, des Arabes et des Persans. L'idée contraire émise par les auteurs européens provient de ce qu'ils ont ignoré ou mal compris le contenu des divers ouvrages qui traitent de la musique et qui sont écrits en arabe, persan et turc. 

Cette idée fausse a, d'ailleurs, motivé l'altération d'autres vérités. Entre autres, Hugo Riemann, dans son Dictionnaire de musique', dit aux mots Arabes et Persans, en parlant du célèbre théoricien turc Alfarabi : « Le plus ancien écrivain musical (chez les Arabes) est Chalil (mort en 780 après J.-C), qui composa un ouvrage sur les rythmes (métrique) et un sur les sons. Au xe siècle, Alfarabi chercha à acclimater dans son pays les théories grecques, mais sans succès. Ce n'est guère qu'au xive siècle qu'apparaissent les premiers écrivains de la Perse, alors que, délivré de l'empire des Turcomans (xie au xive siècle), ce pays passa aux Mongols, sous la domination desquels (Tamerlan) les arts et les sciences prirent un nouveau développement. Le fondateur de la nouvelle école est, il est vrai, un Arabe (!) du nom de Ssaffieddin, dont l'œuvre principale : Schereffiyé, est écrite en langue arabe. Mais on peut citer ensuite : Mahmoud Schirasi (mort en 1314), Mahmoud el Anioul (mort en 1349) 

1. Cf. Terdjrméi-Ibni-Zeydoun, texte turc, page 2S1. Constantinople, 1257 de l’Hégire. 

2. Malheureusement, il n'existe aucun renseignement sur la constitution de ces modes. 

3. Si on ne veut pas accorder cet honneur aux Aryas de la Perse, on peut dire plutôt que la musique est née, comme la langue, avec l'homme, et se trouvait â l'état rudimentaire ; ce sont les anciens philosophes grecs qui ont étudié d'abord les lois qui la régissent. 

4. Il faut remarquer que je préfère ne pas dire ici la théorie de la musique orientale; parce que la théorie expliquée par les philosophes grecs n'était destinée exclusivement ni à l'Orient ni à l'Occident, mais elle visait la science musicale en général, science qui ne devrait pas avoir de patrie. D'ailleurs, en suivant notre monographie on aura la conviction que la musique est, comme les autres sciences mathématiques, une science dont les lois sont fixes et invariables. Comme 2 et 2 font 4 en Orient aussi bien qu'en Occident, les lois fondamentales de la musique sont aussi immuables chez tous les hommes. La divergence de vues qu'on observe chez les théoriciens, dans chaque siècle et dans chaque pays, ne résulte plus ou moins que de leur manque de clairvoyance dans les diverses questions dont l'étude exige une connaissance â la fois théorique et pratique de la musique. 

5. Cf. Traduction française, pages 28 et 29. Paris, 1809. 

[2954]

et Abdulkadir ben Isa (1) (en langue persane).— Le système musical de tous ces écrivains, inauguré en Perse sous la domination arabe, contient, sans aucun doute, les anciens éléments arabes contre lesquels luttait déjà Alfarabi. » 

Celui qui lit les affirmations de M. Riemann serait tenté de croire que les théories de la musique grecque et de la musique arabe sont deux choses très différentes, et que, par conséquent, Farabi a voulu essayer une entreprise absurde comme celle d'appliquer strictement les règles de la grammaire et de la syntaxe de la langue grecque à la langue arabe; la comparaison est la même, et ces allégations sont tout à fait contraires à la réalité. Expliquons notre façon de voir : 

Quels sont donc ces anciens éléments de la musique arabe dont parle M. Riemann? L'ouvrage susdit de Chalil, qui est mort en 170 de l'hégire, n'existe plus aujourd'hui et personne n'en connaît le contenu. Si cet ouvrage arrivait jusqu'à nous, et s'il nous montrait l'existence d'un ancien élément arabe sur la musique, les assertions de Riemann se justifieraient. 

Au contraire, bien que cet ouvrage n'existe pas, nous avons le droit de juger que son contenu était emprunté aux philosophes grecs, parce qu'il est démontré par des documents sérieux qu'avant l'islamisme, les Arabes étaient tout à fait ignorants des sciences et des arts, et qu'en embrassant la religion de Mahomet, ils entrèrent dans une voie de progrès et de civilisation. Quoiqu'il se trouve beaucoup de documents dans les livres orientaux, nous préférons citer ici les paroles suivantes du célèbre orientaliste Hammer, que nous trouvons dans le 2e tome de l'Histoire générale de la musique de Fétis (3) : 

« Une transformation rapide et complète des populations arabes du désert fut le résultat des conquêtes de l'islamisme. Mises en possession de riches contrées où régnait une civilisation relativement plus avancée que la leur, elles perdirent bientôt leur simplicité primitive, se façonnèrent au luxe, à la mollesse, et, s'instruisant par degrés de choses dont elles n'avaient pas même soupçonné l'existence, elles cultivèrent avec succès les sciences, qui leur furent redevables de précieuses découvertes. Dès l'année 132 de l'hégire (749 de l'ère chrétienne), on aperçoit chez les Arabes les commencements de la philosophie; on cite même, de cette époque, un traité du Beau Idéal, dont l'auteur était Ibn Dschafer Ahmed, fils de Youssouf, fils d'Ibrahim (4). Dans le cours du u= siècle de l'islamisme, les sciences ma- thématiques, l'astronomie et surtout l'astrologie, la médecine, la chimie, ou plutôt l'alchimie, la grammaire, la lexicologie, l'histoire, la philologie, sont déjà cultivées avec fruit et comptent un grand nombre d'écrivains. Les Arabes étudient, traduisent et commentent les auteurs grecs, particulièrement Aristote. 

1. Le nom du père d'Abdulkadir est mal écrit ici par H. Riemann . Cela provient peul-être de la faute du copiste du manuscrit. Ce nom n'est pas Isa, mais Gaybi; la ressemblance de ces noms lorsqu'ils sont écrits on caractères arabes est évidente : … Les fautes des copistes ont fait hésiter aussi le célèbre orientaliste Kosegarten pour la lecture de ce nom. Cf. Liber cantilenarum magnum, page 34. Gripesvoldiaé, 1840. Le manuscrit autographe de l'ouvrage d'Abdulkadir qui fait le joyau de ma bibliothèque particulière montre que ce nom est Gaybi.

La musique, qui n'avait été pour eux que le produit d'un instinct original et qui n'avait eu pour interprètes, pendant une longue suite de siècles, que des conducteurs de chameaux et des femmes de condition servile, était devenue une étude sérieuse pour des hommes graves, lesquels s'efforçaient de donner à cet art une théorie rationnelle. Jusque vers le milieu du Ier siècle de l'hégire, on ne trouve pas dans l'histoire le nom d'un seul chanteur, bien que les poètes abondent, tandis que quarante-six chanteuses improvisatrices ont laissé des traces de leur existence au temps de Mahomet et des quatre premiers califes qui lui succédèrent. Des fragments de leurs inspirations nous sont restés (5). Persuadés que la conservation de leur dignité était incompatible avec la profession de musicien, les poètes arabes avaient dédaigné, jusqu'à cette époque, de chanter eux-mêmes leurs vers. Mais sous les règnes des Ommyades (661-734 de notre ère), cet état de choses changea, car, dans cette période du califat, on remarque les noms de plusieurs chanteurs, parmi lesquels se, distinguent Sain Chasir, de Médine, le premier, disent les auteurs arabes, qui joignit sa voix aux sons du luth; Nébith, Ebuth Thahan-el-Kareni et El-Afis, de Damas. C'est aussi dans le même temps que vécut le poète Chalil, à qui l'on attribue un traité du mètre de la versification et le plus ancien livre sur les tons ou modes de la musique arabe. Il mourut à Damas l'an 170 de l'hégire ou 786 de notre ère. » 

Les déclarations ci-dessus montrent amplement que les Arabes, un siècle après leur conversion à l'islamisme, ont commencé à étudier sérieusement toutes les sciences et les arts qui existaient alors. Comme il est évident qu'un peuple désireux de s'instruire s'adresse au pays dans lequel la culture intellectuelle est plus avancée, les Arabes n'ont fait que suivre cette règle, et ils étudièrent avec beaucoup de zèle les auteurs grecs, qui détenaient dans ce temps-là le monopole de la science. C'est bien de ce Chalil que parle M. Riemann comme du premier théoricien de la musique arabe. Son ouvrage contiendrait donc la théorie de la musique telle qu'elle est expliquée par les Grecs, puisqu'il n'y avait pas, comme on le pense, d'ancien élément arabe. D'ailleurs, tous les auteurs orientaux avouent qu'ils ont emprunté aux Grecs la théorie de la musique. Pour en donner un exemple, il suffit de reproduire ici la traduction des premières lignes de la préface de l'ouvrage de Saffieddin (6)  intitulé Schereffiyé : «  Ce traité contient les principes qui sont empruntés, par les anciens, aux philosophes grecs, concernant la science des rapports harmoniques, ainsi que les autres discussions utiles qui ne se trouvent ni dans ces anciens auteurs, ni dans leurs successeurs plus modernes. » Quels sont les anciens dont parle Saffieddin dans la préface de son ouvrage, qui est écrit au milieu du viie siècle de l'hégire (1250 de l'ère chrétienne) ? 

2. Il eût été extrêmement désirable que M. Riemann eût expliqué quels sont ces anciens éléments et quels sont ceux de Farabi qui seraient contraires aux premiers. 

3. Cf. pages 9 et 10. 

4. Hammer-Purgstall, Liiteratur Geschichte der Araber, t. III, p. 37. 

5. Ibidem, t. I, p. 539-570. 

6. Ce théoricien distingué florissait sous le règne du dernier calife abbasside Almusta’sim-Billah. Le manuscrit de son traité est conservé à la Bibliothèque Nationale de Paris, et porte le n° 984 du supplément du fond arabe ; le traité en question a été traduit en résumé par M. le baron Carra de Vaux. Cf. Journal asiatique, n° 7 (1891). 

[2955]

Il est certain que ce sont Chalil tout d'abord, puis Les Frères de la pureté (1), El-Kindi (mort en 248 de l'hégire) (2), Obeidallah ben Abdallah ben Taher (m. en 300 de l'hégire) (3), Al-Farabi (m. en 339 de l'hégire). 

Puisque de tous ces écrits anciens, seuls ceux de Farabi nous sont parvenus, disons qu'il est né vers la fin du iiie siècle de l'hégire, et mort en 339 à Damas (950 de J.-C.) et qu'il s'occupa exclusivement d'emprunter aux traités grecs la théorie de la musique. Ce théoricien a tellement travaillé à éclairer les musulmans par les sciences grecques, qu'il est appelé par les Orientaux le second maître, c'est-à-dire le nouvel Aristote. Le titre de premier maître était déjà donné à Aristote. 

Après Farabi, le célèbre Avicenne, Saffieddin, le célèbre encyclopédiste persan Mahmoud Chirasi (4), Abdtilkadif Méraghi, Mohammed ben Abdul-Hamid-el-lazeki, Molla Djami (5), ont tous parlé de Farabi avec grand respect et s'occupèrent à développer et à expliquer les bases théoriques de cet auteur. 

Prenant en considération que quelques-uns de ces auteurs ont écrit leurs ouvrages en arabe et quelques autres en persan, il ne faut pas supposer qu'ils appartiennent à des écoles diverses et, de là, croire que la musique arabe et la musique persane sont deux choses à part. 

Le savant allemand Kiesewelter est l'un de ceux qui sont tombés dans cette erreur; il a accumulé dans son Die Musik der Araber une multitude d'erreurs, qui sont le résultat de l'hypothèse d'une différence entre la musique de ces deux peuples. Si nous voulions réfuter ces erreurs, cela nous mènerait trop loin de notre sujet, et pour cette raison nous n'insisterons pas. 

II faut savoir que l'islamisme a groupé les Arabes, les Persans et les Turcs en une seule nation, et ces trois nations n'ont eu rien de distinct en matière de langue. Ainsi Farabi, qui était lui-même un Turc, a écrit ses ouvrages en arabe. Au temps de Farabi surtout, la langue turque n'était pas assez perfectionnée; la langue des savants était en premier lieu l'arabe, et puis le persan. 

C'est pour cela qu'à peu près tous les auteurs turcs ont écrit leurs ouvrages ou en arabe ou en persan. Maintenant que nous avons démontré que les Arabes ont emprunté la théorie de la musique aux Grecs anciens, il est temps de dire que les Persans et les Turcs, eux aussi, ont emprunté cette théorie aux mêmes sources. D'ailleurs, pour comprendre que les Arabes ne pouvaient agir autrement, il suffit de considérer que, dans ce temps-là, on regardait la musique comme une science universelle dont les lois étaient les mêmes partout, et on n'avait pas les idées fausses qui ont cours aujourd'hui; par exemple, on ne disait pas que les Arabes divisent l'octave en 17 intervalles, et les Turcs en 24 intervalles et, par suite, que dans la première musique il y a des tiers de ton et dans la seconde des quarts de ton. Ces affirmations singulières étaient tout à fait inconnues des Orientaux, et nous les voyons avec stupéfaction naître chez les Occidentaux. 

On sait peut-être que, d'après la classification des anciens, les sciences mathématiques étaient divisées en quatre sections : 1° la géométrie; 2° l'astronomie; 3° l'arithmétique; 4° la musique. Les musulmans ont emprunté aux Grecs anciens les mathématiques, comme ils leur avaient emprunté les autres sciences. 

Nous voyons même aujourd'hui que les lois fondamentales des intervalles, dont la découverte est attribuée à Pythagore , n'ont pas subi la moindre modification; ainsi, l'intervalle de quinte était représenté par 2/3 au temps de Pythagore, et, après tant de siècles, cette valeur reste la même. Les autres lois conservent intégralement, elles aussi, leur état primitif. 

Cependant, il y a cette différence, que les Orientaux ont bien compris les auteurs grecs et n'ont jamais fait de traductions fautives qui changent essentiellement l'âme d'une phrase. Au contraire, les écrivains occidentaux du xviie et du xviiie siècle qui les ont traduits en latin et en d'autres langues de l'Europe, ont donné lieu à plusieurs malentendus, de par les nombreuses fautes qu'ils ont commises. 

L'argument le plus probant de notre thèse, c'est l'interprétation fautive (6) que les Européens ont faite du système dit grand système ou système complet, qui comprend l'étendue de deux octaves. Nous expliquerons amplement ce point important lorsque nous parlerons de la gamme naturelle des Turcs. Un autre argument vise ce que les mêmes écrivains européens prétendent au sujet des cinq intervalles qui seraient considérés comme les seuls consonants chez les Grecs. Je ne sais pas le grec; mais il n'en est pas moins certain que Farabi, le premier, au X» siècle, et après lui Avicenne (xie s.), Saffieddin et Mahmoud Chirasi (xiiie s.), Abdulkadir (xive s.), Mohammed ben Abdul-Hamid-el-lazeki (xv» s.), ont dit que non seulement l'octave, la quinte et la quarte sont consonantes, mais encore la tierce majeure et la tierce mineure. 

Tous ces auteurs ont pour source les ouvrages de Farabi, et Farabi lui-même a puisé dans les œuvres des philosophes grecs. Si la tierce majeure et la tierce mineure sont déjà proclamées consonantes au xe siècle par Farabi, d'après le contenu des ouvrages grecs, pourquoi donc, quelques siècles après, un encyclopédiste, entre autres, pouvait-il ne pas être au courant de cette vérité et dire que « les Grecs n'admettaient que cinq consonances, savoir: l'octave, la quinte, la douzième, qui est la réplique de la quinte, la quarte et la onzième, qui est sa réplique (7) » ? Il faut donc admettre l'une des deux explications suivantes : ou bien les Grecs considéraient les tierces comme consonantes, ou bien l'honneur de la découverte de la consonance des tierces revient aux Orientaux; mais si Farabi et ses successeurs avaient fait cette découverte, il est certain qu'ils eu parleraient, ainsi qu'il est de leur habitude, comme du résultat de leur propre étude, tandis qu'ils n'en disent rien.

1. Cf. Fétis, ouvrage cité, l. Il, p. 169. Dans cette page, Fétis, en parlant du traité des Frères de la pureté, dit ceci : « On y trouve les divisions du ton par tiers et de l’octave en dix-sept intervalles, comme étant d'un usage pratiqué chez les Arabes. » Pour ma part, j'ai lu tout le traité, et malheureusement, je n'ai trouvé aucun passage formulant ce principe. La prétention de Fétis est donc dénuée de tout fondement. Il est profondément regrettable qu'un savant comme Fétis invente de telles hypothèses pour justifier ses idées préconçues . 

2. Cf. Fétis, p, 11. 

3. Cf. Fétis . p. 166. 

4. Cet auteur et son précieux ouvrage sont cités par M. Riemann. Cf. Dictionnaire de musique, page 484, trad. française. 

5, Ces auteurs classiques ont tous été traduits par moi en turc, et on a commencé déjà à les imprimer à Constantinople avec leur texte arabe et persan en regard de la traduction, sous le titre général : Anciens Auteurs musulmans relatifs à la musique. 6. Par le terme de « l'interprétation fautive » je veux dire qu'on n'a pas bien compris l'ordre des intervalles de ce système complet ; ainsi, à partir du Proslambanomène, on dit qu'il y a ton, demi-ton, ton; tandis qu'il y a Ion majeur, ton mineur, demi-ton majeur. Pour le second tétracorde aussi il y a des fautes commises dans l'interprétation de ce système. 7. Cf. J.-J. Rousseau, Dictionnaire de musique, au mot « Consonance ». 

[2956]

Cette question est très importante, surtout au point de vue de l'histoire de l'harmonie. En effet, ces auteurs orientaux ont expliqué quels sont les sons qui, entendus simultanément, sont consonants. Mohammed ben Abdul-Hamid-el-lazeki, qui vivait en 886 de l'hégire (1481 de l'ère chrétienne), dans son ouvrage intitulé Fet-hié (1) et dédié au sultan Bajazet II, fils de Mahomet, conquérant de Constantinople, dit que « les intervalles consonants sont de deux sortes : les premiers sont formés par l'une des valeurs 8/9, 9/10, 15/16 , 243/256, c’est-à-dire le ton majeur, le ton mineur, le demi-ton majeur ou l’apotome, et le demi-ton mineur ou limma. Les seconds sont formés par l’une des valeurs, 2/3, 3/4, 4/5, 5/6, c’est-à-dire la tierce, la quarte, la tierce majeure et la tierce mineure. Il faut savoir que deux sons musicaux qui ont entre eux l’une des 8/9, 9/10, 15/16, 243/256, si ces sons sont entendus successivement, sont consonants, et s'ils sont entendus simultanément, ils sont dissonants. Tandis que deux sons entre lesquels il y a l'une des valeurs 2/3, 3/4, 4/5, 5/6, sont toujours consonants, soit qu'ils soient entendus successivement, soit qu'ils soient entendus simultanément, u Les Européens ignorèrent ces considérations des théoriciens orientaux jusque vers le milieu du xixe siècle; à ce moment, un savant orientaliste, Kosegarten (2), pour la première fois, en 1840, et après lui Kiesewetter (3), en 1842, donnèrent des renseignements assez étendus, mais insuffisants, sur le contenu de ces ouvrages théoriques de l'Orient musulman. H. Riemann, parlant de la théorie musicale des Orientaux (4), ajoute ce qui suit : 

« Cette théorie est intéressante au plus haut degré, par le fait qu'elle établit la consonance de la tierce majeure, de la tierce mineure, voire des sixtes majeure et mineure, à une époque (au xive siècle, si ce n'est même longtemps auparavant) où les théoriciens occidentaux s'en tenaient encore à la théorie grecque des intervalles. » 

J'apprécie l'exactitude de ces déclarations de Riemann ; mais il n'est pas admissible qu'il continue à croire que la théorie grecque soit différente de celle qui est expliquée déjà dans les ouvrages des Orientaux. Il est suffisamment démontré que les Orientaux n'ont fait que reproduire le contenu des ouvrages grecs; s'il y a une différence à ce sujet entre les Orientaux et les Occidentaux, c'est que les premiers ont bien saisi le sens de ces ouvrages et n'ont pas créé des malentendus comme les Occidentaux. Les détails ci-dessus suffisent pour démontrer que la différence de théorie imaginée par certains auteurs européens n'a existé à aucun temps et n'existe réellement pas aujourd'hui. Maintenant, il reste la question plus importante de savoir si entre les musiques occidentale et orientale il y a vraiment une différence de théorie au point de vue purement mélodique, la question de l'harmonie étant mise de côté. 

IV  Y a-t-il vraiment une différence entre les musiques orientale et occidentale? 

Les anciens philosophes grecs (5) qui ont édifié les premières bases de la théorie musicale n'ont pas divisé cet art en deux sections distinctes sous les noms d'orientale et d'occidentale et n'ont pas, par conséquent, parlé des règles particulières à chaque section, parce qu'ils n'avaient jamais pensé qu'un jour viendrait où la musique serait considérée comme un art dont les règles seraient tout à fait différentes en Orient et en Occident.

1. L'unique exemplaire de cet ouvrage se trouve à la Bibliothèque du Couvent des derviches tourneurs à Yeni-Kapou , en dehors des enceintes de la ville de Constantinople, sous le n° 1243. 

2. Ouvrage cité, 

3. Ouvrage cité. 

4. Cf. Dictionnaire de musique, p. 514. 

5. Si nous regardons les philosophes grecs comme les premiers théoriciens de la musique, cela provient de ce que les plus anciens ouvrages théoriques que nous possédons aujourd’hui sont tous relatifs à ces philosophes. Il est cependant probable que les Grecs, qui aussi, ont profité beaucoup des Egyptiens, qui sont plus anciens qu'eux dans la civilisation; mais puisqu'il ne nous reste rien des égyptiens sur la théorie de la musique, nous avons le droit de considérer les Grecs comme les premiers théoriciens de cette science.

On sait que les premières théories d'une science commencent par la détermination de l'espèce et de la quantité, par la définition des quotités essentielles et accidentelles des éléments qui entrent dans la constitution de cette science. Par exemple, un homme qui désire apprendre une langue doit commencer par connaître les lettres de cette langue. De même, à celui qui veut étudier l'arithmétique on parle du nombre et des espèces de ce nombre. Tout d'abord, quel point de départ devaient adopter les premiers théoriciens qui voulaient jeter les bases de la science musicale? On peut deviner facilement la réponse; mais nous recourons, comme c'est notre habitude, à la voie de l’exemple. Supposons qu'il existe une langue que chacun de nous parle, mais dont la grammaire et la syntaxe ne sont pas encore écrites. Quel est donc le devoir du philologue ? Etudier les règles et les coordonner sous une forme régulière, en un mot, écrire la grammaire et la syntaxe de cette langue. Il n'est pas nécessaire d'expliquer que la musique est aussi ancienne que l'homme ; mais personne ne peut prétendre que la musique des premiers hommes ait été un art complet et bien réglementé. D'ailleurs, quel art est né en possédant le degré de perfection qu'il a acquis avec le temps ? Y a-t-il une chose dans ce monde qui ne soit pas soumise à la loi de l'évolution? Alors, comment pouvons-nous accepter que la musique, constituant une exception à cette règle universelle, soit née chez les hommes à l'état de perfection ? Pourtant, dans les siècles qui se sont écoulés avant les philosophes grecs, et surtout en Egypte, la civilisation était très avancée, et en même temps ce pays avait atteint un haut degré de perfection dans les arts, les sciences et les lettres. Par conséquent, étant donné l'intensité des relations qui existaient alors entre les deux pays de la Grèce et de l'Egypte, on peut admettre que les théoriciens grecs aient trouvé de leur temps, en Grèce, une musique pratique, pouvant être qualifiée de perfectionnée, et qu'ils aient commencé à étudier pour la première fois les règles sur lesquelles cette 

 [2957]

musique est basée, ou bien qu'ils aient travaillé à élargir les notions qu'ils avaient déjà reçues des Egyptiens. Conformément à ce que nous avons dit plus haut, le premier devoir d'un homme désireux de commencer l'étude de la théorie de la musique, était de comprendre quelles sont les lois régissant les sons musicaux qui faisaient partie du chant pratiqué autour de lui. Même aujourd'hui, — mettant de côté les peuples sauvages, — si nous voyageons dans les pays où, dans les temps anciens ou modernes, la civilisation était répandue, nous sommes impressionnés par le chant d'un paysan, doué seulement d'une belle voix et de l'instinct musical, bien que ce paysan n'ait même pas une idée rudimentaire de ce qu'est la musique ; au contraire, le chant d'un autre paysan qui aurait une mauvaise voix et serait dépourvu de l'instinct musical, non seulement ne nous plaît pas, mais déplait aux autres paysans, qui l'invitent au silence. Cela prouve que si le chant humain s'est formé conformément à une loi donnée par la nature, l'homme trouve plaisir à l'entendre; dans le cas contraire, au lieu de plaisir, il ne ressent que de l'aversion. Quelles sont donc ces lois naturelles? Voilà le problème posé par les philosophes grecs, et parmi eux en premier lieu, selon l'opinion générale, par Pythagore. 

Pythagore n'a pas trouvé de moyen plus sûr que de s'adresser à l'intervention des nombres pour exposer les résultats de ses découvertes. Et pouvait-il faire autrement ? Est-il possible d'étudier les phénomènes de la nature sans faire intervenir les nombres qui les mesurent (2) ? 

De notre temps, on voit certains musiciens praticiens qui — on ne sait pourquoi — ne consentent. jamais à l'intervention des nombres dans la musique en disant que nous n'avons rien à faire avec les nombres. Si on juge sans parti pris, cette intransigeance; n'est pas fondée. 

Pour le montrer, supposons un virtuose violoniste ce praticien distingué dira, par exemple : 

«  L'art ne peut être l'esclave des nombres. Moi, je mets mon doigt sur le point où mon instinct musical le conduit. Je ne peux pas évaluer par la pensée la position qui demande le rapport de 25/24 trouvé par les physiciens, comme indiquant l'intervalle que mon doigt franchira pour monter de do b au do #. D'ailleurs, si je veux penser, ce n'est plus de l'art !... » 

Ces prétentions sont-elles justes ? Elles ne le sont pas essentiellement; mais à un autre point de vue, ce violoniste aurait raison, parce que si la théorie de la musique, — comme cela arrive le plus souvent en Europe, — au lieu d'être étudiée et mise à jour par des mathématiciens ou par des physiciens, ne l'était que par des musiciens praticiens, on n'accepterait pas, par exemple, un rapport comme 25/24 qui, ni aujourd'hui ni dans les temps anciens, n'a été pratiqué pour diéser une note, et, dans ce cas, la différence qu'il y a même aujourd'hui entre la théorie et la pratique de la musique moderne n'existerait plus. 

D'autre part, ce violoniste, qui n'est pas aussi libre qu'il le pense dans son jeu, n'a pas raison d'émettre de telles prétentions. Un violoniste doit savoir que les sons qu'il tirera de son instrument demandent entre eux une rigoureuse précision mathématique; de telle sorte que cette précision m\ peut supporter la moindre altération : par exemple, sur le violon si le doigt est mis à deux et même à un millimètre en avant ou en arrière de l'endroit d'où il faut justement tirer un son, les auditeurs aux oreilles sensibles s'écrieront tout de suite : « C'est faux «   

1. Par le mot « ailleurs » je vise les nuances nombreuses du piano et du forte, du crescendo et du decrescendo, de l’accelerando et du rallentando, du lié et du détaché, qui constituent l'accent musical, et dans lesquels réside le secret de la grande impression que la musique éveille dans le cœur de l'homme. 

2. Cf. la Musique, ses lois, son évolution, p. 295-310. Paris 1907.

L'art ne peut donc consister dans la liberté de changer les positions véritables des sons musicaux selon le désir de chacun, mais au contraire dans le respect absolu d'une précision mathématique. Par conséquent, il faut chercher ailleurs' les points sur lesquels l'art pourra baser ses manifestations. 

On pourrait ajouter d'autres considérations pour prouver que les musiciens qui sentent une hostilité à l'égard de l'intervention des nombres dans les questions de théorie musicale se trompent. Je me contenterai de l'exemple ci-dessus. Celui- qui veut approfondir cette question doit consulter l'excellent ouvrage de Jules Combarieu, qui, dans un chapitre intitulé « la musique et les mathématiques », a étudié cette question avec autorité. 

Mais revenons à notre sujet. On sait que Pythagore n'a rien écrit, on s'il a écrit, ses œuvres ne sont pas parvenues jusqu'à nous. Les découvertes qu'on lui attribue sont donc tirées des ouvrages ou des fragments des écrits de ses disciples. S'il reste à établir jusqu'à quel degré les disciples de Pythagore ont pu être les fidèles interprètes de leur maitre, il n'en est pas moins admissible que les modernes qui ont essayé de traduire leurs fragments dans les langues européennes ont commis quelques erreurs pouvant donner lieu à des malentendus. Je puis déclarer avec une conviction qui résulte de longues études sur les auteurs de l'Orient et de l'Occident, tant anciens que modernes, que si Pythagore revenait parmi nous, il n'accepterait pas la plupart des idées qu'on lui attribue, et il déclarerait qu'on a trahi sa pensée. Tout d'abord, examinons les diverses découvertes et les diverses paroles concernant celles-ci qui sont attribuées à Pythagore. Nous savons que les Européens lui attribuent l'invention d'une gamme qui est connue sous le nom de gamme de Pythagore, tandis que les ouvrages orientaux ne contiennent aucune citation à ce sujet. 

Il m'apparait difficile de déterminer le but que se proposent les Européens en lui attribuant cette gamme. Tout le monde sait qu'une gamme est celle qui contient la succession des notes employées dans un mode; par exemple, si nous disons la gamme de la majeur, on comprend la série des notes employées dans cette tonalité. Ou bien, on entend parce terme la gamme naturelle, en d'autres termes la gamme fondamentale d'un système musical et à laquelle on donne aussi le nom de gamme type. 

Quand on parle de gamme de Pythagore, à laquelle de ces deux sortes de gamme se référé l'opinion des Européens? Si on nous répond que c'est au premier sens du mot « gamme », c'est-à-dire que la gamme en question est celle d'un ou plusieurs modes de la musique ancienne, il serait absurde de donner le nom de Pythagore à la gamme d'un mode comme s'il était l'inventeur de celui-ci. 

[2958] 

Je veux dire que si, au temps de Pythagore, un mode, aux notes ordonnées d'après les rapports connus de celle gamme, était chanté par le peuple (1), le devoir de Pythagore se réduisait à analyser ce mode et a. déterminer les rapports existant entre ses noies consécutives. Dans ce cas, la gamme est celle du mode en question, et il n'est pas juste de lui ajouter le nom de Pythagore. 

Si on nous répond que c'est Pythagore qui, pour la première fois, a trouvé les rapports relatifs à la gamme de ce mode, el que de là cette gamme a pris son nom, cette réponse ne nous convaincra pas davantage, puisque les rapports musicaux calculés par Pythagore ne consistent pas uniquement en deux sortes d'intervalles, savoir: l'un, l'intervalle d'un ton =8/9 et l'autre, l'intervalle de limma = 243/256, qui font partie intégrante de la gamme. Surtout, il y a 524288/531441, un intervalle dont le rapport est connu, même de notre temps, sous le nom de comma de Pythagore. C'est Pythagore qui calcula le premier ce comma, dans le but de fixer la différence qui existe entre le ton majeur (8/9) et le ton mineur (59049/65536).

On ne peut pas considérer non plus la gamme de Pythagore comme une gamme fondamentale de la musique ancienne et dont l'inventeur serait Pythagore, puisque les œuvres de Farabi nous montrent clairement quelle était la gamme fondamentale antique el quels rapports existaient entre chaque note. 

En effet, Farabi, après avoir dit que les Grecs donnaient le nom de « système parfait immuable » à l'ensemble des sons qui font partie de leur gamme fondamentale, ajoute que ces sons ont une étendue de deux octaves. 

Il donne en même temps les noms grecs de chacun des quinze sons de ce système en les écrivant dans un tableau avec des lettres arabes. Ce tableau est reproduit de l'ouvrage de Farabi par la plupart des théoriciens orientaux; nous aussi, nous le reproduisons ici, en ajoutant en face de chaque son leur nom moderne et les rapports des sons entre eux calculés par Farabi et ses successeurs : 

Les musicologues occidentaux qui étudieront les noms modernes des notes du système parfait, écrites en face de chaque nom en grec, seront étonnés de voir ce système interprété d'une manière nouvelle. 

Us auront raison, puisque dans presque tous les ouvrages publiés jusqu'à présent en Europe, on trouvait en face de ces noms grecs des notes dont les noms el les intervalles étaient différents. Le tableau suivant donnera une idée des diverses interprétations de ce système en Orient et en Occident. 

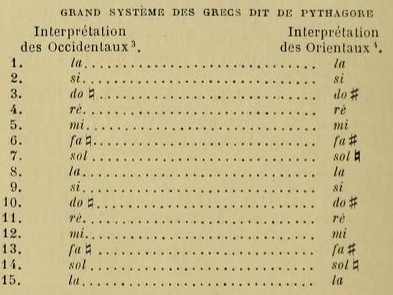
L'abbé Roussier, après avoir inséré ce système dans son ouvrage, ajoute ces lignes : 

« C'est là ce que les Grecs appelloient leur grand système (maximum), le système complet, l'immuable, etc. (perfectum, immutabile, etc.). 

On comprend maintenant que le système parfait serait, d'après les Occidentaux, purement et simplement une gamme de la mineur sans sensible, tandis que, d'après les Orientaux, il serait analogue à la gamme de la majeur sans sensible, ou, en le transposant sur le sot, le même système que l'échelle musicale de Gui d'Arezzo qui commençait par sol et qui était ainsi conçue : 

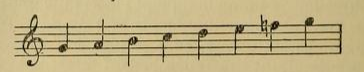
Si les Orientaux et les Occidentaux disent qu'ils ont emprunté le même système aux ouvrages grecs, n'est-il pas étonnant que, des deux côtés, on ait adopté des interprétations si contradictoires? 

Maintenant, réfléchissons un instant que si, dans l'interprétation de la gamme fondamentale d'un système musical, une telle erreur est commise, il est facile de prévoir le nombre des erreurs possibles dans les détails qui suivront. 

En effet, les écrits des Européens sur l'ancienne musique grecque sont tellement remplis d'erreurs et 

1, En effet, ce mode était employé dans l'antiquité de même qu'il l'est aujourd'hui dans la musique orientale; cependant ce mode n'étant pas l'unique mode de l'antiquité, il n'est pas logique qu'un mode, entre tous, ait l'honneur de porter le nom de Pythagore au détriment des autres ! 

2. D'après la traduction latine de Kosegarten : Systematis perfecti disjuncti non mutati. Cf. ouvrage cité, p. 61 et 62. 

3. Cf. surtout l'abbé Roussier, Mémoire sur la musique des Anciens p. 45, Paris, 1770. 

4. Comme nous l'avons indiqué dans le tableau précédent, les Orientaux commencent leur gamme fondamentale par ré et considèrent cette note comme conforme au proslambanomène des Grecs; mais dans ce tableau, nous avons préféré commencer par la, au lien de ré, pour faciliter la comparaison de deux interrelations si différentes. 

[2959]

d'hypothèses non fondées que, s'il fallait les réfuter et les critiquer toutes, cinq volumes comme cette Encyclopédie ne suffisaient pas. 

Cherchons la raison de ces interprétations si diverses du système parlait. 

On raconte que Gui d'Arezzo, croyant, je ne sais pour quelle cause, que la prostambanomène par laquelle commençait le système parfait des Grecs équivalait à un la, cet homme, à qui la musique moderne doit tant, ne trouva pas convenable pour le solfège que la gamme fondamentale qu'il voulait ériger comme base de son système fût une gamme mineure telle que : la. si, do, ré, mi, fa, sol. la, et il jugea à propos d'ajouter un sol au-dessous du la, puisque la prostambanomène des Grecs était équivalente, d'après lui, au la: et, sentant le besoin de donner un nom spécial à ce nouveau son ajouté, il l'appela hypoproslambanomène et le marqua par un gamma de l'alphabet grec : de là vient le nom de la gamme (1). 

Si cette anecdote est vraie, telle est bien la source de l'interprétation erronée du système parfait des Grecs par les Européens. Cependant, il faut constater que, parmi tant de mauvais interprétateurs, il s'en trouva un qui entrevit la vérité. 

C'est M. Alphonse Heegmann (2), qui, en parlant du diapason de la musique grecque, effleure cette question dans le passage suivant : 

« La note la plus basse du système ancien était la prostambanomène du trope hypodorien. Mais l'échelle mobile ayant été remplacée par une échelle fixe, comme le voulait la simplicité de la musique d'église, la proslambanomène, marquée de la lettre romaine A, ne désigna plus que cette seule note; et Gui d'Arezzo en lit le bi, placé aujourd'hui entre la 1e et la 2e ligne de la portée armée d'une clef de fa. Il y ajouta une note, un soi, à un ton au-dessous. Méibomius prétend que les Grecs l'avaient déjà (3) sous le nom hypoproslambanomène, mais qu'ils la négligeaient comme obscure ou manquant d'ampleur. » 

Quoi qu'il en soit du résultat. Gui d'Arezzo n'était pas loin du système parfait des Grecs, puisque son échelle de sol :

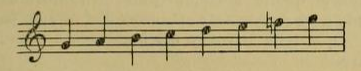
était identique à l'échelle fondamentale antique. 

Toute l'erreur se résumait dans le fait de dire que la proslambanoméne équivaut au la, et de là découlait l'interprétation du système parfait des Grecs comme une gamme de la mineur ainsi écrite : 

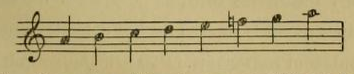
Mais, d'un autre côté, si nous considérons les détails donnés par H. Riemann dans le paragraphe "Lettres de l'Alphabet" de son Dictionnaire, Gui d'Arezzo n'avait nullement besoin d'ajouter un son au-dessous du la, parce qu'avant lui les lettres A, B, C..., employées comme notation par des théoriciens occidentaux, signifiaient déjà, non pas, comme aujourd'hui, la, si, do..., mais do, rè, mi... Ce qui revient, en transposant, et au point de vue mélodique, à l'échelle de sol de Gui d'Arezzo : 

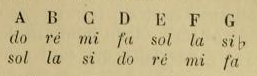
Nous reproduisons ici, pour plus de clarté, les déclarations de Hiemann à ce sujet : 

« C'est au xe siècle seulement que nous voyons apparaître un nouveau système de notation alphabétique, composé des sept premières lettres de l'alphabet latin : A B C D E F G, correspondant aux sept sons de l'échelle diatonique (Cf. "ecclésiastiques"); mais il convient d'ajouter que la signification de ces lettres différait de celle que leur donne aujourd'hui la nomenclature allemande, puisqu'elles correspondaient à notre échelle ut ré mi fa sol la si. » 

Si, d'après l'assertion de Hiemann, au x» siècle, les lettres A B C... signifiaient la, ré, mi..., comme je le pense, cela veut dire que l'intonation du système parfait des Grecs, dans ce temps-là, n'était pas encore perdue; dans ce cas, pourquoi Gui d'Arezzo aurait-il été obligé d'ajouter un r pour lui donner la couleur du mode majeur qu'elle possédait déjà ? 

Je ne sais comment on pourrait concilier deux faits aussi contradictoires. Ce qu'il y a de certain, c'est que le système parfait des Grecs a pu conserver sa constitution antique à travers les siècles, malgré les diverses interprétations. 

Les vues et les idées des musiciens occidentaux sur la gamme paraissent très curieuses et incompréhensibles aux yeux des Orientaux. Par exemple, on parle de plusieurs gamines sous les noms de gamme de Pythagore, de Ptolémée, d'Aristoxéne, de Zarlino, des physiciens. C'est bien ! Mais est-il permis à chacun de pouvoir constituer une gamme selon son propre désir et de demander aux hommes de chanter d'après les proportions de cette gamme ? Si personne ne peut le faire, d'où viennent donc ces différentes gammes? 

Nous avons expliqué plus haut que le devoir d'un théoricien est de mesurer le chant des hommes, d'en dégager les lois, et non pas de rédiger à priori une gamme artificielle composée des rapports qu'il lui plaît d'adopter. Donnons un exemple pour éclairer notre opinion ; si nous livrons la même eau minérale à divers chimistes, en leur demandant de l'analyser soigneusement, il est certain que le résultat de leur examen sera le même, si toutefois leur capacité scientifique est égale. C'est ainsi que devraient agir les théoriciens à qui incombe le devoir de faire l'analyse musicale. 

Puisque nous avons plusieurs résultats dus à divers théoriciens et à divers siècles, il y a deux probabilités : ou bien les théoriciens n'ont pas un égal degré de capacité, ou bien le chant humain a subi des modifications au cours de chaque siècle! 

Si l'on admet que, dans les rapports des sons musicaux entrant dans la composition du chant humain qui sont fixés par les anciens théoriciens, il n'a pu survenir réellement que de légères modifications à travers les siècles, on peut soutenir avec raison qu'il y a une gamme mélodique (5) donnée universellement 

1. Cf. J.-J. Rousseau, Dictionnaire de Musique, au mot Hypoproslambanoménos. 

2. Cf. Examen de la théorie musicale des Grecs, pages 78 et 79, Lille. 1852. 

3. La vérité, c'est que les Grecs avaient cette note, non pas sous le nom de hypoproslambanomène, mais sous celui de proslambanomène. 

4. Cf. ouvrage cité. p. 460. 

5. Nous sommes de l'avis que la gamme mélodique et la gamme harmonique sont deux gammes bien différentes qu'il ne faut pas confondre. 

[2960]

aux hommes par la nature, et que cette gamme a conservé depuis les temps anciens son état originel. Les interprétations contradictoires de quelques théoriciens résultent sans aucun doute de leur manque de clairvoyance des faits qui sont soumis à leur examen. 

Pour appuyer notre opinion, étudions chacun des principaux intervalles musicaux avec leurs rapports respectifs fixés par les anciens et les modernes : 

1° L'octave. — Pythagore disait que si on met un chevalet mobile juste à la moitié d'une corde tendue, et si on fait vibrer la seconde moitié de la corde, le son rendu par la seconde moitié est bien l’octave du son donné par la corde entière; il en résulte que le rapport de l'octave est de 1/2 . Depuis Pythagore, les siècles se sont écoulés, et cependant ce rapport reste toujours le même; personne n'a prétendu le contraire. 

2° La quinte. — Pythagore disait que si on fait vibrer les deux tiers d'une corde tendue, en en retranchant le tiers par un chevalet, le son obtenu sera la quinte du son donné par la corde entière; de là le rapport de la quinte, 2/3. Ce rapport est aussi adopté par tout le monde. 

3° La quarte. — Pythagore disait encore qu'en faisant vibrer les trois quarts d'une corde tendue, en la raccourcissant d'un- par un chevalet, le son obtenu sera la quarte du son donné par la corde entière; par conséquent, le rapport de la quarte est 3/4. Jusqu'à présent, personne n'a prétendu que la race humaine fît entendre la quarte autrement que dans le rapport ¾ (1).

4° La tierce. — Je serai obligé de parler un peu longuement de cet intervalle. D'abord, remarquons que le nom de tierce est un nom moderne qui lui a été donné. Les Européens ont désigné ainsi un intervalle toujours composé de deux degrés, c'est-à-dire de trois sons diatoniques. Chez eux, si la tierce est composée d'un ton majeur 8/9 et d'un ton mineur 9/10, elle prend le nom de tierce majeure = 4/5, et au contraire, si la tierce est composée d'un ton majeur 8/9 et d'un demi-ton majeur =15/16, elle prend le nom de tierce mineure 5/6.

Les anciens Grecs ne connaissaient pas d'intervalle dénommé tierce; au lieu de la tierce, ils avaient le diton. Puisque dans la musique grecque, qui était une musique essentiellement mélodique, on employait deux sortes de tons, l'un majeur et l'autre mineur, il était tout naturel que le diton fût de deux espèces : 

1° 8/9 x 8/9 = 64/81

2° 8/9 x 9/10 = 4/5

Le rapport de 4/5 était le rapport approximatif de la 2e espèce de diton, composé d'un ton majeur et d'un ton mineur : quant à son vrai rapport, il était : 

9/8 x 59049/65536 = 8192/8561

Mais, comme nous l'avons dit plus haut, les Grecs ne faisant pas usage des sons simultanés, la tierce n'avait ni importance ni nom particulier; elle prenait seulement le nom de l'intervalle plus ou moins grand dont elle était formée. 

Par conséquent, on ne voit pas pourquoi les Occidentaux ont envisagé la question de la tierce d'un tout autre point de vue. Ils ont, sans aucune raison, donné le nom de tierce pythagoricienne au rapport 64/81, et de tierce naturelle au rapport 4/5, et ensuite, ils ont voulu savoir par des expériences quelle est celle de ces deux espèces de tierce qui est employée dans la musique moderne! Si la question était résolue radicalement, pouvait-on sentir le besoin de faire ces expériences? Je ne le crois pas. 

Pour bien comprendre la raison pour laquelle les Occidentaux se sont égarés à ce sujet, il suffit de considérer que, dans une musique mélodique, l'exigence d'un mode demande quelquefois que deux tons majeurs 8/9 x 8/9 soient employés l'un après l'autre; mais un autre mode aussi demande qu'après un ton majeur, l'autre ton soit mineur (8/9 x 9/10 ). Dans ce cas, la tierce du premier mode se trouve dans le rapport de 64/81, et celle du second mode se trouve dans le rapport approximatif 4/5. (On sait déjà que son vrai rapport est 8192/8561) Ce sont là des exigences d'une musique purement mélodique (2) comme celle des Grecs, et par suite il n'est pas juste de dire, en parlant de n'importe quelle musique (puisque toute musique orientale ou occidentale est basée d'abord sur la mélodie), que telle tierce y est employée à défaut de l'autre. 

Quant à la question de savoir quel rapport doit exister entre deux sons entendus simultanément, lorsqu'il y a entre eux l'intervalle de tierce majeure, nous répondrons ceci : l'harmonie n'étant pas employée chez les Grecs, on voit, dans les ouvrages des anciens théoriciens orientaux, que les deux sons ayant entre eux le rapport de 4/5 et entendus simultanément, sont consonants. Et les Orientaux ayant emprunté la théorie de la musique aux Grecs, les théoriciens orientaux se contentent de relater simplement ce phénomène : si ces théoriciens avaient fait une découverte d'une telle importance, ne le proclameraient-ils pas avec orgueil? Partant de ce point 

1. Un professeur nommé M. F. -A. Renaud a cependant proposé de remplacer le 3/4 par 16/21 ; mais il va sans dire que ce sont là des rapports chimériques calculés au cabinet, et non de vrais rapports obtenus en écoutant la voix humaine. Cf. son ouvrage intitulé le Principe radical de la musique et la Tonalité moderne, p. 151, Paris, 1870. 

2, C'est cette nécessité mélodique qui a fait déclarer à MM. Mercadice et Cornu, lors de leurs célèbres expériences, que la gamme de Pythagore est celle de la mélodie. Mais, en faisant cette déclaration, ces auteurs ont oublié que la musique cultivée par Pythagore n'était pas exclusivement composée de deux sortes d'intervalles, savoir ; du ton majeur (8/9 ) et du limma (243/256), comme parait l'établir la constitution de la gamme qu'on lui attribue, mais que dans cette musique on employait aussi le ton mineur (59049/65536) l’apotome (2048/2187).

[2961]

de vue, nous n'hésitons pas à confirmer que les Grecs savaient que si entre deux sons, entendus simultanément, se trouve le rapport de n, ces sons produisent une consonance. 

Toutefois, il importe de remarquer que si les Grecs connaissaient les sons dont l'audition simultanée est consonante, ils ne connaissaient et ne pratiquaient point l’harmonie telle que nous la concevons aujourd'hui. 

Nous avons un autre argument plus important pour montrer que les Grecs connaissaient la consonance des tierces. Cet argument est basé sur ce que les anciens Grecs comptaient la musique parmi les sciences mathématiques, et de là, comme nous l'avons vu plus haut, lorsque nous avons reproduit un passage de la préface de l'ouvrage de Saffieddin, la musique portait aussi le nom de Science des rapports harmoniques. 

On sait que, chez les anciens, il y avait trois sortes de proportions, savoir : la proportion arithmétique, la géométrique et l'harmonique. 

C'est cette science des rapports qui détermine et fixe le rang que les intervalles doivent occuper au point de vue de la consonance et de la dissonance l'un envers l'autre. Cette science des rapports est expliquée longuement par les mathématiciens grecs, surtout par Euclide, que les Orientaux n'ont fait que traduire textuellement (1). 

D'après la science des rapports, le premier en ordre de tous les rapports est le rapport du double 2: 1 qui donne l'octave; le second, est le rapport de 3 : 2 qui donne la quinte; le troisième, est le rapport de 4 : 3 qui donne la quarte; le quatrième, le rapport de 5 : 4 qui donne la tierce majeure; elle cinquième, le rapport de 6 : 5 qui donne la tierce mineure. 

La science des rapports nous apprend encore que l'octave est la consonance par excellence; la consonance de la quinte est un peu faible relativement à l'octave; ainsi, la consonance s'affaiblit graduellement à mesure que l'intervalle devient plus petit. 

Ceci admis, on devine facilement l'absurdité des observations suivantes qu'on rencontre au mot Pythagore du Dictionnaire de Riemann : 

«  Pour les Grecs, la tierce avait été et était toujours (?) un intervalle dissonant (!); soit que l'on n'admit pas pour elle le rapport 4 : 5, soit que ce rapport ne parût pas assez simple pour être placé au même rang que 1:2, 2:3, 3:4, comme consonance. » 

C'est une erreur; on a admis pour la tierce le rapport 4/5 comme rapport approximatif, et le rapport 8192/8564 comme rapport juste dans la mélodie ; en même temps, elle est considérée comme consonante, mais le rang de sa consonance vient après celui de la quarte d'après l'ordre naturel de leurs rapports : 4 : 3 (quarte) et puis 6: 4 (tierce). 

Pour résumer les détails ci-dessus sur la tierce, disons que la musique des Grecs était une musique purement mélodique, et que par conséquent leurs premiers théoriciens, ou Pythagore si l'on veut, n'ont pas attaché beaucoup d'importance à l'intervalle que nous connaissons aujourd'hui sous le nom de tierce; ils se contentèrent simplement de nommer diton l'intervalle qui se composait de deux tons. Le- diton avait, certainement, les deux formes suivantes : 

8/9 x 8/9 = 61/81

8/9 x 59049/65536 = 8192/8561

Mais cet intervalle ne jouait pas un rôle essentiel dans la mélodie, comme aujourd'hui dans l'harmonie; les Grecs n'ont pas même pensé, en le divisant en deux espèces, à désigner chacune d'elles d'un nom spécial. 

Plusieurs siècles après, les musiciens occidentaux, à leur tour, ont constaté, par suite de nombreuses expériences et par la découverte du phénomène de la résonance, que, dans la musique harmonique, ce sont les tierces majeures ayant entre elles le rapport de 4/5 qui seules sont consonantes. Pour cette raison, les physiciens ont justement accepté le rapport 4/5 comme le vrai rapport de la tierce majeure. 

Cependant, malgré plusieurs avis contradictoires à ce sujet, an peut soutenir qu'il y a une gamme mélodique et aussi une gamme harmonique; la tierce, dont le rapport est 4/5, appartient donc à la gamme harmonique. Au contraire, la voix humaine, lorsqu'elle chante une mélodie, fait l'une des deux choses suivantes : ou bien elle emploie deux tons majeurs comme consécutifs (8/9 x 8/9=64/81), ou bien elle emploie, de ces deux tons, le premier majeur (8/9) et le second mineur (59049/65536),  ce qui fait : 

8/9 x 59049/65536 = 8192/8561

Nous pouvons donc donner au premier rapport (84/61) le nom de tierce majeure ditonique, et au second rapport (8162/8561) le nom de tierce majeure mélodique. Comme nous le verrons ci-après, Pythagore, qui connaissait le rapport du ton majeur 8/9, n'ignorait pas non plus que le ton mineur était plus petit que le ton majeur, dans le rapport d'un comma (524288/ 531 441) et que d'autre part le ton mineur était composé de deux limmas 

243/256 x 243/256=59049/65536

Si nous ne voulons pas accepter ces vérités, serait-il pas absurde de qualifier le rapport 524288/531441 de comma de Pythagore? 

Donc, on peut prétendre avec raison que, même dans la question de la tierce, il n'y a, en réalité, aucune divergence essentielle de vues entre l'Orient et l'Occident depuis les temps anciens jusqu'à nos jours, parce que les Orientaux qui acceptent 

1. Kiesewetter, dans son ouvrage intitulé « Die Musik der Araber » a donné assez de détails sur cette science des rapports qui est la base de la théorie mathématique de la musique. Cependant Riemann, dans le mot messel de son Dictionnaire, se trompe lorsqu'il dit que cette théorie est l'invention des Arabes et des Persans ; tandis que cette science des rapports à laquelle Riemann donne improprement le nom de théorie du messel est tirée des ouvrages d'Euclide et des autres mathématiciens grecs, par les Orientaux. Cf. Dictionnaire de musique, le mot messel, p. 514 et 515. 

[2962]

certainement aujourd'hui (1) le rapport 4/5 comme celui de la tierce harmonique, ont reconnu depuis l'antiquité ce même rapport comme le rapport approximatif de leur tierce majeure mélodique qui est dans le rapport de 8561/8192.

Les Occidentaux, cultivant une musique purement harmonique, se sentaient obligés d'employer essentiellement les tierces majeures dans le rapport de 4/5, rapport un peu plus grand que la tierce mélodique des Orientaux (8192/8561), tandis que l'exigence du tempérament a obligé les Occidentaux à employer des tierces majeures encore un peu plus grandes que le rapport 4/5. (On sait que, dans le tempérament égal, l'intervalle qui éprouve le plus de changements de place est la tierce mineure, et après elle, la tierce majeure.) 

Voilà pourquoi les Occidentaux ne peuvent goûter la saveur très fine et très délicate de la tierce majeure mélodique des Orientaux (8192/8561).

Pourtant, les expériences de MM. Mercadier et Cornu ont prouvé que les Occidentaux emploient aussi la tierce dite pythagoricienne, dont le rapport est de 64/81. Cela prouve que la mélodie exige quelquefois l’emploi de la tierce (8192/8561), tandis que l’emploi de la tierce majeure (4/5) est toujours obligatoire dans l’harmonie.

En acceptant ce résultat, tous les malentendus concernant la question si controversée des tierces se dissipent. 

Quant à la tierce mineure, cet intervalle est, depuis Pythagore, chez les Orientaux, composé d'un ton majeur et d'un limma : 

8/9x243/256=27/32

Les théoriciens orientaux lui ont donné le rapport juste de 27/32 et le rapport approximatif de 5/6. 

D'ailleurs, les physiciens occidentaux, tout en travaillant beaucoup à rendre uniformes toutes les tierces mineures, n'ont pas réussi à réaliser cet idéal, et comme la tierce mineure (fa/ré) ne s'est pas trouvée conforme au rapport 5/6, ils ont dû accepter seulement pour cette tierce le rapport 27/32.

Avouons ici qu'en effet, par exemple, les notes ré et fa naturel entendues simultanément devraient avoir entre elles le rapport de 5/6 pour qu'elles fussent consonantes; mais s'il s'agit de la mélodie, alors ce rapport de 5/6 cède toujours la place au rapport de 27/32. Une tierce mineure, soit qu’elle se compose d’un ton mineur et d’un demi-ton majeur :

59049/65536 x 2048/2187=27/32

Soit qu’elle se compose d'un ton majeur et d’un limma, comme :

8/9 x 243/256=27/32

doit toujours être, en mélodie, dans le rapport de 27/32 . 

5° Le ton majeur. — Pythagore connaissait-il cet intervalle ou non ? Cette question est, elle aussi, controversée parmi les Occidentaux. 

M. Louis Laloy prétend (2) que Pythagore connaissait seulement l'octave (1/2), la quinte (2/3). la quarte ( 3/4), et ignorait le ton majeur (8/9); voici comment il s'exprime : 

«  L'acoustique pythagoricienne, qui seule nous intéresse ici, partit de l'expérience fondamentale du monocorde; en mesurant les longueurs des cordes qui donnent les trois consonances d'octave, de quinte et de quarte, on trouva entre ces longueurs des rapports fixes et définis : 2/1, 3/2, 4/3. Telle fut la découverte de Pythagore. Rien ne nous autorise à supposer qu'il ait connu également le rapport 9/8(3/2 :4/3), qui représente le ton majeur, c'est-à-dire l'excès de la quinte sur la quarte. » 

Cependant M. Laloy, un peu plus loin dans son ouvrage (3), s'exprime ainsi : « Le rapport 9/8, que Pythagore ignorait sans doute, fut découvert d'assez bonne heure, puisque Philolaüs le connaît. » 

On reconnait bien que ce rapport est cité dans les écrits du disciple de Pythagore, mais sans que soit précisé à qui appartient l'honneur de la découverte, puisque cet honneur, d'après lui, n'appartient pas à Pythagore. Quel est donc l'homme de génie qui, venant au monde immédiatement après Pythagore et immédiatement avant Philolaüs, a pu découvrir ce fameux rapport de 9/8 ?

Selon nous, émettre une telle assertion à l’encontre d'un philosophe comme Pythagore, fondateur d'une école qui avait pour devise : » Tout est fait de mesures, de poids, de nombres (4), » et dire que « Pythagore connaissait les rapports 2/3 et 3/4 et ignorait cependant le rapport 8/9, quoiqu'il soit la déduction de ces deux rapports », revient tout à fait à dire, en parlant d'un arithméticien distingué, qu'il connaît les nombres 3 et 4, mais qu'il ne connaît pas le nombre 1, qui est la différence des deux nombres précédents! 

1. En effet, j'ai plusieurs fois remarqué que lorsque les musiciens des cafés, qui n'ont aucune idée Je ce qu'est l'harmonie, jouent tous à l'unisson, l'un d'eux, se soumettant à l'instinct, fait des accords composés seulement de deux sons comme sol-si, ou do-mi. Cela prouve que les Orientaux trouvent plaisir à des sons simultanés, et que par conséquent le sens harmonique est commun à tous les hommes. 

2. Cf. Aristoxène de Tarente et la Musique de l'antiquité , p. 49, Paris, 1904. 

3. Cf. Le même ouvrage, p. 52. 

4. Cf. Ed. Chaignet, Pythagore et la Philosophie pythagoricienne, tome II, p. 3 et 4, Paris, 1873. 

[2963]

Les auteurs modernes (1) parlent d'un instrument qui serait inventé par Pythagore sous le nom de Octochordum Pythagorae ou Lyre pythagoricienne; l'inventeur d'un octocorde pouvait-il ignorer ce ton? 

D'ailleurs, la plupart des auteurs anciens et modernes affirment clairement le contraire de l'opinion de M. Laloy. Entre autres, M. Vincent, dans sa traduction des fragments de l’Hagiopolite (manuscrit de la Bibliothèque royale de Paris, du xii'' au xiii" siècle, coté n" 3601, après avoir parlé de la fameuse expérience de Pythagore dans l'atelier du forgeron, dit ceci : 

« Encouragé (Pylhagore) par ce résultat, il construisit avec quatre cordes un instrument qu'il nomma une musique, et dont il porta depuis le nombre des cordes jusqu'à sept. C'est à ce sujet que Philolaüs, pythagoricien, dans un ouvrage qu'il adressait à une dame professant les mêmes doctrines, pour lui exposer les principes de la philosophie harmonique, s'exprime ainsi : « L'étendue de l’harmonie [octave] comprend la syllabe [quarte] et la dioxie [quinte]; et la dioxie surpasse la syllabe dans le rapport sesquioctave [c'est-à-dire d'un ton] (2). » 

En plus de ces paroles de Philolaüs, nous rencontrons dans un ouvrage traduit par Ch.-Em. Ruelle (3) le passage suivant, qui éclaire complètement cette question en faveur de notre thèse ; nous ne pouvons résister au désir de le reproduire textuellement : 

(Troisième division du Canon.) 

« 1. — Pythagore tendait une corde, puis, la divisant en neuf parties, suivant la notation de certains points, il frappait le sou lui-même en particulier (c'est-à-dire la corde elle-même dans sa totalité), et il trouva ainsi le proslambanomène. 

« Ensuite, faisant abstraction de la neuvième partie, il frappa la corde sur huit parties et reconnut que cette corde sonnait l'hypate des hypates, laquelle note comportait un intervalle de ton (par rapport à la corde totale); et il conçut le ton comme étant dans le rapport sesquioctave ou rapport de 9 à 8. » 

Le célèbre théoricien turc Farabi déclare, lui aussi, d'après les anciens auteurs grecs, que «  l'excédent de la quinte sur la quarte s'appelle ton ». Kosegarten traduit en latin ce passage de Farabi par les lignes suivantes : 

« Propterea igitur id, que ab quinario quaternarium superatur, intervallum reditus adpellatur. Veteres vero hoc spalium et intervallum sonans vocabant. »

Les trois citations précédentes nous dispensent, croyons-nous, de donner d'autres arguments pour prouver que Pythagore connaissait bien le rapport de 9 à 8. 

6° Le ton mineur. — Disons tout de suite que Farabi et ses successeurs, lorsqu'ils parlent du ton majeur, auquel ils donnent le nom de   [], n'ajoutent pas que ce ton majeur a une autre espèce de ton plus petit que lui, connu sous le nom de ton mineur. Ces théoriciens appellent  [], ce que nous nommons le ton mineur; M. le baron Carra de Vaux traduit ce terme par le mot » externe »; Kosegarten» par le mot « latéral », et Land'' par le mot « voisin » ; nous préférons la traduction de Land.  

L'appellation de cet intervalle (ton mineur) par le nom de » voisin » est le résultat de ce que la position des touches (ligatures) sur le manche du luth   [],  a été prise en considération; par exemple, on avait mis une ligature sur le- de la 1er corde du luth accordée au ré 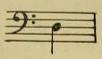  [],   pour désigner la place sur laquelle il faut mettre le doigt afin d'obtenir mi#; comme c'était l'index qui touchait cette ligature, on lui a donné le nom de ligature de l'index. Cependant, si on désirait, à partir du même ré, obtenir un ton mineur, il fallait raccourcir approximativement d'une dixième de la corde entière, et la ligature de ce ton mineur était très rapprochée de celle du ton majeur; voilà pourquoi cette dernière ligature a pris le nom de voisine de l'index, et de là, l'intervalle qu'elle représentait a été désigné aussi par le nom de l'intervalle voisin    [], Les praticiens du luth avaient encore mis une autre ligature à partir du ré, dans le rapport de 2048/2187, pour le ré# ; cette ligature portait aussi le nom de voisine, mais, pour les distinguer, la 1ere a été nommée    [], « grande voisine » (59049/65536) et la 2e a été nommée   « petite voisine » (2048/2187).

Nous n'avons jamais douté que Pythagore connût l'intervalle de grande voisine (ton mineur), puisqu'il est généralement admis que Pythagore connaissait le ton majeur et le comma 524288/531441 lequel porte encore son nom et n'est autre chose que la petite différence qui, ajoutée au ton mineur, en faisait un ton majeur. Ne serait-il pas illogique de prétendre que celui qui a fait la soustraction d'un comma du ton majeur si compliqué, ignorait le ton mineur qui en est le reste : 

59049/65536 x 524288/531441= Ton mineur x Comma = Ton maj. 

7° L'apotome. — C'est le nom ancien de l'intervalle auquel on donne aujourd'hui le nom de demi-ton chromatique. Les Occidentaux, ne voulant pas accepter que Pythagore soit le premier calculateur de cet intervalle, sont enclins à reporter cet honneur sur le disciple du grand philosophe. Il n'y a aucune raison pour soutenir une telle idée, puisque Philolaüs, dans les fragments qui restent de ses écrits, se garde bien de s'attribuer la qualité de calculateur du rapport de Vapotome qui est 2048/2187, et qu'il se contente d'exposer, en fidèle disciple, la doctrine de son maître. Il résulterait d'ailleurs des explications données 

1. Cf. Pierre Lichtenthal : Dictionnaire de musique, tome II, p. 110, Paris. 1839. 

2. Cf. Notices et extraits des manuscrits de la Bibliothèque du roi, tome XVI, p. S69 et ;T1. Paris 1847. 

3. Introduction harmonique de Cléonide, la division du Canon d'Euclide le géomètre, Canons harmoniques de Florence, page 64, Paris, 1SS4 (troisième volume de la Collection des auteurs grecs relatifs à la musique). 

4. Cf. Kosegarten. Alii Ispahanensis Liber cantilenarum magnus, p. 47 et 48, Gripesvoldiae. 1840. 

5. Cf. ouvrage cité. Extrait du Journal Asiatique, p. 56. 

6. Cf. ouvrage cité, p. 85. 

7. Cf. Recherches sur l'histoire de la gamme arabe, p. 103, Leyde, 1834. 

[2964]

ci-après sous le n° 8, que Pythagore, après avoir trouvé l'intervalle nommé limma (243/256), fut amené à savoir ce qui resterait d'un ton majeur après eu avoir soustrait ce limma ; les déclarations suivantes de M. Henri Martin (1) viennent à l’appui de notre thèse : 

« Les anciens Pythagoriciens s'appliquèrent à trouver les formules arithmétiques de ces trois genres fondamentaux (diatonique, chromatique et enharmonique). Ils pensèrent que, pour cela, il fallait partir des intervalles donnés par la division de la quarte en tons pleins. Or, nous connaissons déjà le ton et le limma. Mais voici quelques autres intervalles qui en dérivent. 

Le limma étant moins de la moitié du ton, on nommait apotome, l'autre partie, dont la valeur est 2187/2048 ; car 2187/2048 x 256/243 = 9/8. »

Il est regrettable que le rôle que l’apotome joue en réalité dans la théorie des dièses et des bémols n'ait pas attiré comme il faut l'attention des physiciens. On sait que ceux-ci prétendent que, pour surélever ou pour abaisser d'un demi-ton mineur une note quelconque, il faut la multiplier par 25/24 ou par 24/25. Cette théorie est-elle tirée des usages des musiciens? Je ne le crois pas. Puisque toute théorie devrait provenir de la pratique, pourquoi les physiciens ont-ils conçu pareille théorie, laquelle apparaît tout à fait contraire à l'usage des praticiens ? C'est à eux de répondre. Si les hypothèses des physiciens étaient réalisées, voyons comment l'intervalle do-ré, par exemple, serait divisé : 

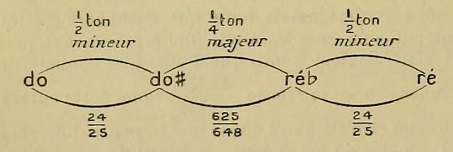
Comme on le voit, d'après les allégations des physiciens, le demi-ton do-do# serait plus petit que le demi-ton dot#-ré. Dans la pratique, au contraire, j'ai plusieurs fois remarqué que les musiciens européens emploient le demi-ton chromatique do-do#, plus grand que le demi-ton diatonique do#-ré. 

La raison en est que les dièses déterminent ordinairement des notes sensibles, et que celles-ci tendent toujours à se rapprocher de l'octave. Le musicien, cherchant à satisfaire son oreille, fait, lorsque son instrument le lui permet, le demi-ton do#-ré: moindre que la moitié juste d'un ton, et, par là, l'intervalle do-do # se trouve agrandi; Il en est de même du bémol, qui tend toujours à descendre vers la note inférieure, et alors ré-réb se trouve plus grand que ré b-do. 

Les praticiens occidentaux, qui ont saisi cette différence entre la théorie et la pratique, et qui s'abstiennent d'employer les nombres, ont voulu remédier à cet inconvénient d'une manière pratique et facile à comprendre. Ils ont dit que le ton est divisé en linif parties égales dont chacune prend le nom de comma. Lorsqu'une note est diésée, cela veut dire qu'elle est haussée de cinq commas; et quand elle est bémolisée, cela signifie qu'elle est abaissée également de cinq commas :

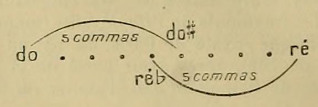
En parlant ainsi, les praticiens admettent le contraire de la théorie des physiciens ; c'est-à-dire que pour le demi-ton chromatique (do-do #) ils proposent le rapport 25/27, et pour le demi-ton diatonique (do#-ré) celui de 24/25, ce qui est d'ailleurs très conforme à leur pratique : 

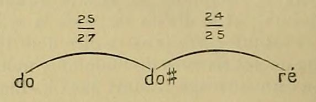
Maintenant, il est impossible de ne pas rappeler une fois de plus les paroles si justes d'un simple accordeur de pianos, mais qui pourtant voyait clairement la véritable loi à laquelle étaient assujettis, les sons employés en musique : 

« Si les physiciens avaient donné au dièse le rapport de l'apotome 2187/2048 , au lieu du rapport 25/24, la théorie aurait été d'accord avec la pratique, et le ton se serait divisé en deux demi- tons correspondant à l'apotome et au limma, qui sont précisément égaux, à très peu de chose près, aux demi-tons, chromatique et diatonique pratiqués (3). » 

C'est ce vœu de Montal qui avait été exaucé, il y a des siècles, par Pythagore; en effet, ce théoricien, en partageant le ton en deux demi-tons, l'un majeur dans le rapport de 2048/2187, et l'autre mineur dans le rapport de 243/256 , n'avait fait autre chose que de mettre au jour une loi à laquelle la voix humaine obéissait alors et obéit encore. 

Tout ce qu'on a dépensé de temps et d'encre depuis, sur cette question si simple et si définitivement résolue, est donc allé au vent ! 

8° Le limma. — C'est le nom ancien de l'intervalle auquel on donne aujourd'hui le nom de demi-ton diatonique. L'intervalle de quarte 3/4 une fois calculé par Pythagore, il s'agissait de diviser d'abord la quarte en des tons majeurs. Pythagore, après en avoir retranché deux tons majeuis, a vu qu'il restait quelque chose de plus petit que la moitié d'un ton. Il calcula (4) son rapport et trouva qu'il était dans le rapport de 243/256; il le nomma lemma. 

1. Cf. Etudes sur le Timée de Platon, p. 410, Paris, 1841. 

2. Cf. Cours de physique, par M. Jamin, tome III, 1er fascicule (Acoustique), p. 18, Paris, 1887. 

3. Cf. l' Art d'accorder soi-même son piano, par C. Montal, p. 178, Paris, 1836. 

4. M. Laloy, qui ne croit pas que Pythagore puisse déduire le rapport de 8/9  comme l'excès de la quinte sur la quarte, ajoute, à l'appui de sa thèse, après le passage de son ouvrage que nous avons reproduit plus haut, les lignes suivantes : « Il (8/9) se déduit directement des précédents (2/3 et ¾), mais à la condition que l'on sache qu'une différence d'intervalles s'exprime par un quotient de rapport ; et nous verrons que cette loi particulière, si elle a été observée par un grand mathématicien comme i-luclide, n'a jamais été formulée expressément dans l'antiquité et qu'elle n'a pas encore d'action, en particulier, sur certains calculs de Philolaüs. » On peut demander ici à M. Laloy comment Pythagore a pu exprimer la différence d'intervalle qu'il y a entre la quarte et le diton par le rapport de 243/256, ceci étant le quotient de leur rapport respectif 3/4 : 64/81=243/256 

[2965]

Farabi a traduit ce mot grec par []   qui signifie aussi le reste en arabe. 

Comme il résulte des expériences de MM. Mercadier et Cornu, les artistes européens, en jouant une mélodie, emploient des intervalles pythagoriciens. Donc le limma a une raison d'être lorsqu'on établit la théorie de la musique ou du chant humain. 

Pour reconnaître cette raison d'être, il suffit d'attacher un peu d'attention aux mélodies populaires créées spontanément par l'instinct naturel des nations. Par exemple, examinons cette mélodie : 

 

Si on joue ces notes sur le violon, en se soumettant à l'exigence du goût musical, on sent l'obligation de ne mettre qu'un intervalle de limma entre les notes mi-fa et la-si b. 

Par cette expérience, on reconnaît que l'intervalle mi-fa# n'est pas toujours, comme le prétendent les physiciens, dans le rapport de 15/16, et on constate encore qu’en mélodie, après deux tons majeurs, il est toujours nécessaire d'employer un demi-ton égal à 243/256 . De même pour l'intervalle la-si b, puisque, à partir de fa, vers l'aigu, on emploie deux tons majeurs successifs fa-sol et sol-la, il est nécessaire, pour compléter la quarte juste de fa-si b, d'employer le demi-ton la-sib égal à un limma 243/256.

***

Après avoir lu les pages précédentes et après avoir exclu de notre esprit certaines assertions des auteurs occidentaux selon lesquelles il y a quart de ton ou tiers de ton dans la musique orientale, livrons-nous aux réflexions suivantes : 

Qu'est-ce que c'est que la musique ? C'est sans doute un don précieux fait par Dieu aux hommes pour charmer nos âmes. N'est-ce pas aussi elle qui établit en nos cœurs l'accord parfait des bons sentiments? Quel but universel et juste se propose-t-elle ? Un poète français distingué tel que Gilbert dit : 

«  L'Harmonie de l'Univers c'est l'unité de la nature. Tous les peuples ont chanté le Créateur! Glorifiez votre Dieu par vos chants, mortels qui vivez : car lorsque vous aurez disparu, les races futures accorderont leurs voix et leurs instruments de musique pour célébrer le Dieu de l'Univers. » 

Est-ce qu'on peut soutenir que Dieu a créé les hommes de l'Orient et de l'Occident avec des caractères sensibles qui diffèrent les uns des autres ? Si on veut en croire Fétis, il faudrait affirmer une telle hypothèse ! En effet, le célèbre musicographe, en parlant de l'aptitude musicale des peuples d'Orient, écrit la singulière observation suivante (1), qu'il nous faut reproduire pour réfuter convenablement l'idée fausse qu'elle contient : 

« Il est donc aussi démontré, par ces faits indiscutables, que les intonations antidiatoniques sont agréables aux populations orientales, et que le mélange de toutes ces intonations, de proportions différentes, n'a rien qui les blesse. La cause de ce penchant est dans le caractère sensuel de petits intervalles de son (2), et dans le rapport de ce caractère avec l'organisation physique des peuples de l'Asie. » 

Il est vraiment difficile de préciser quelles sont ces intonations antidiatoniques dont parle Fétis, parce que, d'après ce que nous savons déjà, il n'y a pas d'intonations semblables dans la musique orientale. 

Pourquoi a-t-on donné le nom de diatonique à la musique européenne, et pourquoi cette même musique n'est-elle pas qualifiée de ditonique ? Etudions d'abord celle question. 

La musique européenne est qualifiée de diatonique parce qu'elle n'est pas basée sur une gamme fondamentale comme la gamme de Pythagore, composée uniquement de deux tons majeurs, d'un limma, de trois tons majeurs et d'un limma. Au contraire, elle est basée, d'après ce qu'on pense généralement, sur une gamme type composée d'un ton majeur, d'un ton mineur, d'un demi-ton majeur; puis d'un ton majeur, d'un ton mineur, d'un ton majeur et encore d'un demi-ton majeur. Par exemple, donnons ces deux gammes avec leurs rapports respectifs : 

Gamme ditonique et gamme diatonique

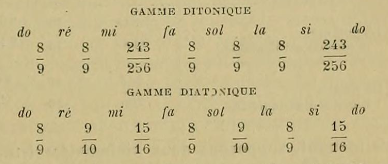
Il résulte de la seconde gamme qu'en réalité la musique européenne (3) n'est pas exclusivement composée de tons et de demi-tons, comme elle est pratiquée généralement aujourd'hui, par suite de l'acceptation universelle du tempérament égal. Au contraire, dans la constitution des modes majeur et mineur, il y a non seulement les tons majeur et mineur, mais encore les demi-tons majeur et mineur. 

Cette base une fois acceptée, on ne com-oil pas une thèse plus absurde que celle consistant à dire que les intervalles de la gamme juste, véritablement employés par les Européens, sont diatoniques, et que ceux qui sont employés par les Orientaux sont antidiatoniques, parce que, comme il a été démontré

1. Cf. Fétis, ouvrage cité, tome II, p. 370 et 371. 

2. Lorsqu'il s'agit de la musique orientale, on répète toujours que cette musique est composés de petits intervalles. Je ne connais pas la raison de cette légende, puisque le plus petit intervalle qu'elle emploie est le limma, dont le rapport est 243/256 ; et aucun intervalle plus petit que le limma n'y est employé mélodiquement. Tandis que, s'il faut en croire les physiciens occidentaux, le demi-ton mineur de la musique européenne a le rapport de — qui est sans doute plus petit que 243/256.

Alors, quelle est celle de ces deux musiques qui est composée de petits intervalles ? 

3. Nous visons ici la musique occidentale considérée au point de vue purement mélodique. 

[2966]

suffisamment plus haut, ces intonations de proportions différentes que Félis croit seulement réservées à la musique des Orientaux sont cependant en réalité identiques à celles qui sont employées dans les mélodies occidentales jouées sur les instruments à justesse absolue, comme le violon, ou chantées par la voix juste d'artistes de talent. 

Afin de permettre de comparer facilement les rapports acceptés par les musiciens de l'Orient et de l'Occident, pour les huit principaux intervalles musicaux que nous avons étudiés plus haut, nous donnons le tableau suivant : 

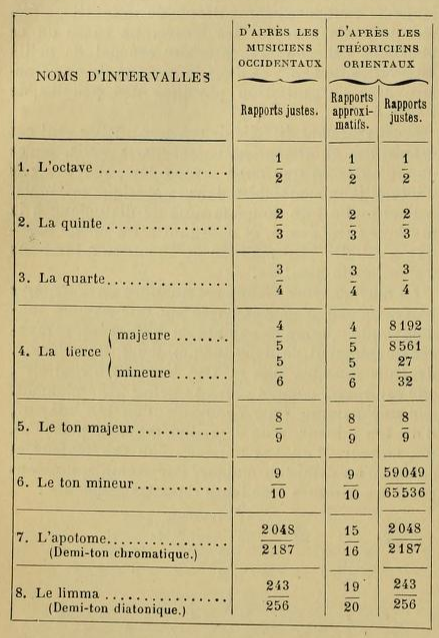
Maintenant, supposons deux violonistes virtuoses dont l'un soit un Oriental et l'autre un Occidental, et proposons à ces artistes d'exécuter l'un après l'autre ces huit intervalles musicaux à partir du la (2° corde), avec cette condition expresse de s'affranchir complètement du sentiment harmonique, et de se soumettre au seul sentiment mélodique. 

Comme on le comprend par l'examen du tableau ci-dessus, ces deux violonistes, lorsqu'ils exécutent l'octave, la quinte et la quarte du la (2e corde libre), qui est le point de départ, ne laissent percevoir entre eux aucune différence d'intonation. 

En ce qui concerne le n° 4, pour jouer le do# qui est la tierce majeure du la, nos deux violonistes seront d'accord, à condition que le violoniste européen ne donne pas un doit tempéré ou harmonique. 

1. Cependant, pour que le violoniste oriental joue un si, à partir du la, dans la proportion de 8/9, il faut ajouter à ce si un demi-dièse ; parce que dans la gamme fondamentale de la musique orientale l’intervalle la-si # est un ton mineur. Mais comme il y a certains modes orientaux dans lesquels on emploie après 1r la un si dans le rapport du ton majeur, on a senti la nécessité de distinguer ce dernier si en le faisant précéder d'un demi-dièse. 

Lorsqu'ils jouent do#, qui est la tierce mineure du la, il y a deux probabilités pour le violoniste européen : 1° s'il se propose que ce do# soit, avec la chanterelle mi, dans la proportion de tierce majeure harmonique (4/5), l'intervalle la-do# aura la proportion de 5/6, et dans ce cas, le do#, joué par le violoniste oriental dans le rapport de 27/32 à partir du la, et dans le rapport de 64/81 avec le mi #, se trouvera un peu grave relativement au do # du violoniste européen ; 2° si ce dernier violoniste se propose de jouer un do# qui soit la quarte juste du soi il qu'on obtient sur la 3e corde du violon, on ne trouvera alors aucune différence entre les do# des deux violonistes; et dans ce cas, la proportion qui se trouvera entre ce do# et mi# de la chanterelle ne sera pas égale à 4/5, mais bien à 64/81.

Comme il n'y a pas de différence entre les théoriciens occidentaux et orientaux au sujet du rapport du ton majeur qui est 8/9), les deux- violonistes à qui on proposera de jouer un ton majeur à partir du la seront tout à fait d'accord. 

Lorsque nos violonistes jouent le n° 6, c'est-à-dire le ton mineur, si le violoniste européen ne tend pas à ce que le si # soit la tierce majeure harmonique du sol de la 3e corde, les si# de nos artistes seront à peu près (2) d'accord. 

Quant à l'apotome et au limma qui forment les n° 7 et 8, le violoniste européen, pour s'élever d'un demi-ton majeur à partir du la, ou, en d'autres termes, pour diéser le la, donnera un la# dans le rapport de 15/16, ou plutôt, comme l'a si justement prétendu M. Montai, donnera un la# dans le rapport de 2048/2187 ; de même, pour s'élever d'un demi-ton mineur à partir du la, ou, en d'autres termes, pour jouer le si #, il franchira un intervalle dans le rapport de 24/25 ou plus justement de 243/256 ; on arrive à ce résultat que, pour diéser ou bémoliser une note, les violonistes des deux pays sont d'accord. 

Pourtant, on ne saurait trop répéter que le violoniste à qui on proposera ces expériences devra s'attacher à ne pas employer les sons artificiels de la gamme fausse dite tempérée ainsi que les intervalles de la gamme harmonique, l'emploi de ces sons constituant pour les Européens une sorte de seconde nature dont il leur est difficile de se défaire. 

D'ailleurs, certains praticiens occidentaux, qui se sont occupés de la théorie de la musique, ont très pratiquement résolu la question de la détermination des valeurs des signes d'accidents, qui est conforme à la réalité. En effet, ils disent à ce sujet : 

«  Un ton renferme neuf commas ; il y a donc, dans un ton, un demi-ton de 4 commas, c'est le diatonique, et un de 5 commas, c'est le chromatique. » 

2. Je dis « peu près , parce que, d'après mes observations, ù l'exception de certains modes, les praticiens orientaux sont généralement enclins à employer les tons mineurs plutôt dans le rapport 9/10 (rapport approximatif) que dans le rapport 59049/65536, qui est le rapport juste, déterminé par Pythagore. 

[2967]

Dans ce cas, s'il nous est permis de les traduire en nombres, les idées des praticiens occidentaux donnent le résultat suivant : 

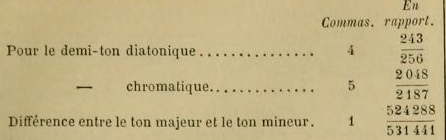
Par contre, les physiciens européens, au lieu d'accepter les rapports véritables ci-dessus, qui sont pratiqués à la l'ois chez les Occidentaux et Orientaux par les voix et par les instruments, ont déterminé les trois autres rapports suivants, et ont établi ainsi une divergence éternelle entre la théorie et la pratique de la musique: 

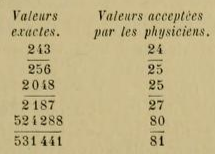
Comme les praticiens occidentaux négligent la différence qu'il y a entre les tons majeur et mineur, la division précédente du ton en 4 et 5 commas s'appliquerait certainement à l'intervalle de ton majeur. Quant à la division du ton mineur, selon notre idée, elle obéit à deux lois : 1° si la valeur du Ion mineur est reconnue comme égale à 9/10, on le divise ainsi : 

 

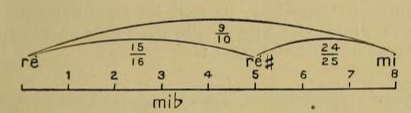
2° si on accepte, comme les théoriciens orientaux,  la valeur du ton mineur mélodique égale a 59049/65536, alors sa répartition s'opère, conformément à la pratique, de la façon suivante : 

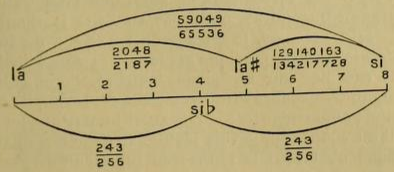
Une fois qu'on a compris la loi véritable qui régit les intervalles musicaux employés par les Occidentaux et les Orientaux, on reconnaît facilement combien Fétis s'est trompé dans ses déclarations reproduites plus haut au sujet des intonations antidiatoniques qui auraient existé, d'après lui, dans le chant des Orientaux. Pour affirmer l'existence de ces soi-disant intonations antidiatoniques dans la musique orientale, Fétis va même jusqu'à prétendre que la cause de ces intonations est dans l'organisation physique des peuples de l'Asie; ce qui est très étonnant! 

Le lecteur qui a suivi cotte longue dissertation a eu, je crois, la conviction que nul art de l'Orient n'est plus méconnu en Europe que la musique orientale. 

La barriére qui sépare l'Orient de l'Occident au point de vue musical ne consiste pas, comme on le croit généralement, dans la divergence des intervalles de ces deux musiques; il faut chercher ailleurs l'origine de cette barrière. Nous l'expliquerons ci-dessous, en répondant à une objection supposée. 

D'ailleurs, il n'est pas juste de croire à l'existence d'une semblable divergence, puisque « la vérité en musique est une » ! Les rapports des huit principaux intervalles désignés dans le tableau ci-dessus sont ceux de la musique employée en Orient et en Occident depuis les temps anciens jusqu'à nos jours; ils n'ont subi aucune modification à travers les siècles, et dorénavant n'en subiront aucune, moins que la forme actuelle des organes qui produisent la voix humaine et les lois physiologiques qui les régissent soient changées! 

***

Ici, on peut, nous faire l'objection suivante : 

Puisque la vérité en musique est une en Orient et en Occident, pourquoi un Européen qui voyage en Orient trouve-t-il la musique orientale très étrange et complètement incompréhensible? De même, pourquoi un Oriental ne s'intéresse-t-il pas à la musique occidentale, lorsqu'il l'entend pour la première fois? 

D'après ce que nous pensons, ce phénomène comporte plusieurs causes, et ces causes varient pour chacun des deux auditeurs. Cherchons d'abord pourquoi un Occidental n'éprouve pas de plaisir à l'audition de la musique orientale : 

l" L'oreille d'un Occidental, depuis son enfance, est habituée à entendre le plus souvent les notes uniformes de la gamme fausse dite tempérée. Cette habitude peut, jusqu'à un certain point, éteindre le sentiment de la mélodie avec lequel naissent les hommes. 

Par exemple, on sait que l'intervalle entre l'ut et le ré ? n'étant pas égal en réalité à l'intervalle ré-mi, l'effet ut-ré n'est pas identique à l'effet ré-mi ; de même, les demi-tons chromatique et diatonique diffèrent l'un de l'autre. Si ce raisonnement est appliqué à un morceau tout entier, on arrive à cette conclusion que certaines finesses musicales, qui trouvent leur explication naturelle dans une plus grande diversité d'intervalles musicaux, sont perdues, et que le caractère musical du morceau est notablement modifie. La plupart des Européens sont habitués à entendre une semblable musique. 

2° Un Occidental, depuis son enfance, na pas entendu peut-être une seule fois une mélodie sans son accompagnement et, par suite, il n'est pas habitué à goûter la saveur particulière que possède une mélodie exécutée avec de purs intervalles mélodiques; la mélodie seule, entendue dans ces conditions, lui paraîtra très nue, et en outre, les intervalles mélodiques justes n'exerceront aucune influence sur son ouïe mal éduquée (1). 

1. Ici, il m'est impossible de ne pas me souvenir de l'anecdote suivante, rapportée par Fétis dans le 2e tome de son Histoire de la musique (p. 27) comme un exemple de la puissance de l'habitude dans les modifications de notre sentiment de l'art : 

« Le célèbre organiste M. Leramens, né dans un village de la Campine, y faisait, dans sa première jeunesse, ses études musicales sur un clavecin depuis longtemps horriblement désaccordé, aucun accordeur ne se trouvant dans le pays. Par une circonstance heureuse, il arriva qu'un facteur d'orgues fut appelé pour faire des réparations à celui de l’abbaye d'Everbode, située près de ce village : le hasard le conduisit chez le père du jeune musicien, et lui fournit l'occasion d'entendre celui-ci jouer de son misérable instrument. Choqué de la multitude d'intonations fausses qui frappaient son oreille, le facteur prit immédiatement la résolution d'accorder le clavecin ; mais, quand il eut fini cette opération, M. Lemmens en éprouva les sensations les plus désagréables : il ne retrouva qu'après un certain temps le sentiment des rapports justes des sons, égaré par la longue habitude de rapports différents. »

Je crois que les Européens qui entendent pour la première fois la musique orientale se trouvent dans la situation de M. Lemmens. 

[2968] 

3° Les chanteurs orientaux emploient toujours la voix de tête; à un Occidental habitué à entendre les chanteurs européens qui chantent toujours en voix de poitrine, la manière de chanter des Orientaux semble tout à fait anormale (1). On est même allé jusqu'à qualifier le chant oriental de miaulement de chats ! 

Par contre, il existe des raisons pour qu'un Oriental ne trouve pas de plaisir à entendre la musique occidentale : 

1° Un Oriental, dont l'oreille est assez délicate pour sentir la très petite différence qu'il y a entre le ton majeur (8/9 ) et le ton mineur (9/10), ne peut pas être satisfait lorsqu'il entend les noies uniformes de la gamme tempérée. 

2° Un Oriental, qui est habitué à entendre une musique toujours à l'unisson, ne peut pas distinguer, entre l'enchaînement des accords, surtout lorsqu'ils sont produits par les notes fausses de la gamme tempérée, la mélodie qui est pour lui le but suprême de la musique; par conséquent, ce pêle-mêle de sons ne lui procure aucun plaisir. 

3° La manière de chanter des Occidentaux en voix de poitrine paraît être contraire au goût esthétique des Orientaux; un passage qu'on lit dans l'ouvrage de Blainville dépeint très exactement les impressions d'un Oriental vis-à-vis d'un chanteur européen. En effet, cet auteur se trouvant à Constantinople, et ayant chanté à un musicien turc certains morceaux occidentaux, lui demanda comment il les trouvait; le musicien turc aurait donné la réponse suivante : « D'abord, il me semblait entendre crier au feu, et le mélange de sons que vous trouvez si merveilleux ne faisait qu'un bruit confus à mes oreilles (2)... » 

Telles sont les causes qui ne permettent pas aux Orientaux et aux Occidentaux de goûter leurs musiques respectives et qui excusent leurs sentiments réciproques à ce sujet. 

On peut nous faire une seconde objection; en effet, un Occidental peut nous dire ceci : 

« J'admets volontiers que les Occidentaux n'aient pu étudier convenablement la musique des Orientaux; mais que faut-il penser des déclarations de savants comme Bourgault-Ducoudray qui, voyageant en Orient, et se mettant en contact avec les musiciens indigènes, ont recueilli de leur propre bouche des détails théoriques qui paraissent tout à fait incompatibles avec les données énoncées dans les pages précédentes? Par exemple, dans son ouvrage intitulé Etude sur la musique ecclésiastique grecque, le savant en question, parlant du second mode de l'église grecque, donne l'échelle suivante : 

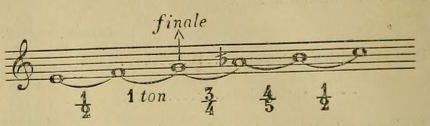
comme ambitus de ce mode, et ajoute en même temps que « ce qu'il y a de caractéristique dans le second mode, ce qui fait naître chez l'auditeur européen une impression intolérable si le chanteur chante faux, et bizarre s'il chante juste, c'est la présence d'un la fixe, trop bas d'un quart de tort, qui produit entre sol et la un ton trop petit, et entre la et si un ton trop grand... Comment concilier ces données avec les vôtres ? »

Je réponds simplement que le mode en question n'est pas exclusivement employé par les néo-grecs dans leurs églises, mais qu'il est au contraire très populaire en Orient, et par conséquent connu de tous les peuples de l'Orient depuis plusieurs siècles. Cependant, les théoriciens de la musique ecclésiastique grecque sont tellement en désaccord entre eux, tant dans les temps anciens que dans les temps modernes, que, même aujourd'hui, il y a une musique ecclésiastique grecque pratiquée et plusieurs théories de la même musique; la théorie expliquée à l'honorable Bourgault-Ducoudray est l'une de ces diverses théories (4). 

Quant aux rapports vrais des intervalles dont se compose l'échelle du 2e mode ci-dessus donnée par Bourgault-Ducoudray, ils sont les suivants; seulement je transpose cette échelle une quinte plus haut, comme on écrit en Orient : 

N'est-il pas surprenant, en effet, que l'honorable Bourgault-Ducoudray n'ait pas vu dans la quarte sol — la b — si — do, le tétracorde supérieur du ton de do mineur de la musique moderne? Si cette échelle était exécutée sur un piano tempéré, l'oreille de Bourgault-Ducoudray trouverait-elle cet intervalle de seconde augmentée (la bi — si #) aussi bizarre que lorsqu'il est chanté par la voix juste (4) ? Je ne le crois pas, puisque c'est bien le tétracorde supérieur du mode mineur. Dans ce cas, la faute du chanteur oriental consiste dans l'emploi des intervalles mélodiques 

1. Il faut cependant reconnaitre que la manière de chanter en usage chez les Orientaux et qui consiste à chanter en voix de tête, est la plus convenable pour la musique orientale qui met en usage tous les intervalles mélodiques justes. On prétend même qu'avec la voix de poitrine, l'intonation de ces divers intervalles serait très difficile, sinon impossible, et que le ton et l'accent donnés par les artistes orientaux à leur chant conviennent mieux si l'exigence des langues orientales. Mon ami le Révérend l'ère J. Thibaut, des Augustins de l'Assomption, qui a habité â Constantinople plusieurs années et dont la compétence en fait de musique orientale est considérable, partage mon idée â cet égard. 

2. Cf. Blainville, Histoire générale, critique et philologique de la musique, Paris, 1767, p. 60. 

3. Cf. page 25. 

4. En 1905, je m'adressai à Sa Sainteté Joachim III, patriarche orthodoxe de Constantinople, dans le but d'étudier moi-même la musique de son Eglise. Ce sympathique chef de l'Eglise avait bien voulu me désigner le protopsalte (1er chantre) de l'église patriarcale pour me donner tous les détails possibles sur cette musique. Plus d'un an, régulièrement deux fois par semaine, j'ai fréquenté le Patriarchat du Phanar, où m'attendait le protopsalte M. Yacobos, mon professeur de musique ecclésiastique. Ces visites assidues m'ont donné la conviction que cette musique n'est autre chose que la musique dite orientale, et tant de théories étranges qui lui sont attribuées ne sont que de pures inventions de certains soi-disant théoriciens. 

5. Si le chanteur grec avait expliqué à Bourgault-Ducoudray  qu'entre sol et la b il y a un intervalle de demi-ton chromatique, composé de cinq commas, tout malentendu pouvait été évité. 

[2969]

justes dont les rapports sont écrits au-dessous de la même échelle transposée sur si#, comme on le voit plus haut. 

Cet exemple prouve amplement que, pour une oreille habituée aux sons de la gamme tempérée, fût-ce celle d'un éminent musicien comme Bourgault-Ducoudray, il devient très difficile de saisir la saveur d'intervalles mélodiques purs. Mais il est juste de reconnaître à ce sujet la responsabilité des soi-disant théoriciens indigènes grecs qui ont induit en erreur le célèbre musicien. 

***

Avant de finir ce chapitre, qui a pour but de démontrer qu'il n'y a pas en réalité de différence, au point de vue mélodique, entre les musiques orientale et occidentale, je dois ajouter quelques observations. 

On sait que les tons entiers qui entrent dans la constitution de la gamme d'un mode ne sont pas tous des Ions majeurs; quelques-uns d'entre eux sont majeurs et quelques autres sont mineurs. En effet, la gamme du mode majeur de la musique européenne est conforme à cette loi mélodique, puisqu'elle est composée d'abord d'un ton majeur, puis d'un ton mineur, etc. 

Cependant, comme on néglige la différence entre le ton majeur et le ton mineur, il en résulte que la musique européenne perd beaucoup de son expression mélodique. Par exemple, pour transposer à un ton plus bas les notes : 

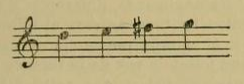
on se contente de les écrire sous cette forme : 

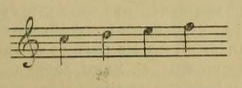
tandis que, d'après les rapports qui se trouvent entre les notes de ces deux échelles, rapports qui sont fixés parles physiciens occidentaux eux-mêmes, ces échelles ne devraient pas être tenues, au point de vue mélodique, pour identiques entre elles, puisqu'elles ont les rapports suivants : 

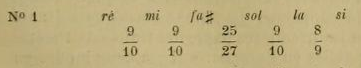
Voilà pourquoi, si les intervalles rê — mi et mi — fa# de notre exemple sont en réalité des tons mineurs, il va sans dire qu'en transposant ces deux intervalles, qui ont certainement leur forme spéciale d'expression, sur les notes : 

do ré mi 

composées au contraire d'un ton majeur et d'un ton mineur, on détruit cette l'orme spéciale d'expression, parce que transposer, c'est reproduire un air avec les mêmes intervalles, en élevant ou en abaissant toutes les notes sans leur faire subir aucune modification, si minime soit-elle. 

On sait encore que dans certaines mélodies les deux tons majeurs se succèdent; dans ce cas aussi, s'il s'agit de les transposer, il ne faut pas faire l'un d'eux majeur et l'autre mineur. 

Vous me direz : « Comment cela est-il possible? » Je réponds qu'il ne suffit pas de reconnaître théoriquement qu'il y a un ton majeur et un ton mineur ; il faut les employer en pratique comme ils sont déjà pratiqués par les voix justes. 

Dans la musique orientale, on prête beaucoup d'attention à la différence entre tons majeurs et mineurs. Aussi la transposition est-elle considérée, parmi les praticiens orientaux, comme une des questions les plus difficiles. Lorsque les praticiens veulent sonder le degré de capacité d'un musicien, ils lui posent une question sur la transposition et en demandent la réalisation, parce qu'un artiste qui est habitué à jouer d'ordinaire un mode, par exemple sur la tonique la, s'il se trouve obligé de jouer le même mode sur la tonique si, tout en respectant la succession des tons majeurs et mineurs, des apotomes et des limmas, manifeste le plus grand embarras, alors que cette transposition lui deviendrait facile s'il pouvait, comme en Europe, ne se préoccuper que des tons et des demi-tons. Pour mieux m'expliquer, j'apporterai un nouvel exemple; il démontrera à la fois l'importance de la différence qu'il y a entre les tons majeur et mineur, et l'inexistence d'une différence, au point de vue mélodique, entre la musique orientale et occidentale. Je prends comme exemple l'air de Au clair de la lune, qui est connu de tous. Je le transcris en sol majeur : 

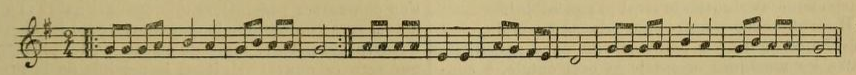
Si nous examinons cet air, nous voyons qu'il consiste en une mélodie composée dans la limite d'une sixte dont la note grave est ré et la note aiguë est si. D'après les rapports désignés par les physiciens occidentaux, entre les notes de cette mélodie ainsi notée, se trouveraient les chiffres suivants : 

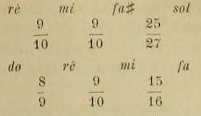
Si nous accordons un piano d'après les rapports ci-dessus et si nous jouons l'air en question, nos oreilles entendront une mélodie tout à fait étrange. 

Cependant, un musicien oriental qui prend en considération la constitution mélodique de cet air, n'hésite pas à juger qu'entre les notes du môme air doivent se trouver les rapports suivants : 

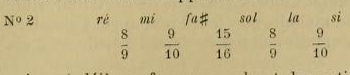
qui sont déjà conformes au chant des artistes à voix juste. 

En prenant deux pianos, si on accorde les cordes du premier d'après les rapports n° 1, et celles du second d'après les rapports n° 2, et si l'on joue l'air Au clair de la lune, on constatera que les notes du second piano sont conformes au bon goût artistique, et très semblables à l'effet que produit cet air lorsqu'il est chanté par la voix humaine. 

[2970]

Ajoutons aussi que nous pouvons très bien transposer cet air sur n'importe quelle note à notre choix ; mais pour cela il est strictement nécessaire de respecter ses rapports essentiels tels qu'ils sont indiqués sous l'échelle n° 2. Pourtant est-ce possible, dans l'état actuel des instruments de musique fabriqués en Europe ? Transposons, par exemple, cet air en do majeur ; il devient : 

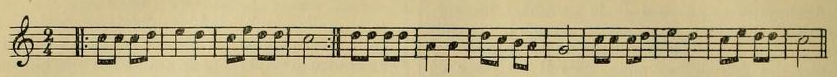
Si nous jouons cet air sur un instrument à tempérament, comme, avec ce système, toutes les notes sont d'ailleurs plus on moins dénaturées, il est impossible de reproduire la mélodie pure dans n'importe quel ton que ce soit; renonçons donc à jouer cet air sur un instrument de ce genre. 

Mais si nous jouons la mélodie ci-dessus sur des instruments de justesse absolue comme les cuivres naturels et à coulisse, aurons-nous réussi par cette transposition en do majeur à conserver à cette mélodie son caractère essentiel? On ne peut pas donner une réponse affirmative à cette question, puisque dans ce nouveau ton de do majeur la sixte de sol mi, dans laquelle la mélodie est enfermée, aurait pour intervalles, d'après les physiciens occidentaux, les rapports qui suivent : 

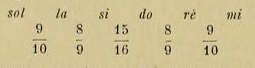
Dans ce cas, on voit que la sixte ré-si n" 2 et la sixte sol-mi ne sont pas identiques en leurs intervalles, puisqu'elles ont pour rapports respectifs : 

Maintenant, réfléchissons à ceci : un artiste qui chante cet air en sol majeur et qui entonne dans cette tonalité les notes ré-mi-fa #, en mettant d'abord un ton majeur puis un ton mineur, cet artiste, pour chanter le même air en do majeur, changera-t-il la place de ces tons pour mettre le ton mineur d'abord et le ton majeur ensuite? Evidemment non, le changement de ton n'ayant aucune influence sur la modification du caractère mélodique d'un morceau. 

Cet exemple montre avec certitude que si les instruments de musique ne sont pas en état de réaliser la différence qu'il y a entre le ton majeur et le ton mineur, la transposition d'une mélodie dans un ton quelconque avec justesse n'est pas possible (1). 

Il résulte encore autre chose de cet exemple, c'est l'évidence qu'il n'y a point de différence essentielle entre les musiques orientale et occidentale, à condition qu'on accepte des deux côtés la vérité mélodique. L'air intitulé Au clair de la lune n'est pour nous ni oriental ni occidental, mais c'est tout simplement une mélodie que tout homme peut chanter^ avec les intervalles désignés dans l'échelle n° 2 ci-dessus. 

Il y a cependant, ainsi que nous l'avons répété plusieurs fois, cette petite différence : les théoriciens orientaux, en se conformant à un proverbe qui dit : « Il coupe le poil en quarante parties, » ont si minutieusement analysé le chant humain qu'ils ont dû accepter les rapports de l'échelle n° 2 comme les rapports approximatifs des intervalles qui se trouvent entre les notes de cette échelle. La différence entre les vrais rapports et les rapports approximatifs est la suivante : 

 

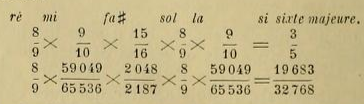
Quelle différence reste-t-il donc entre les musiques orientale et occidentale au point de vue mélodique? S'il s'agissait, en fin de compte, d'accepter, au lieu des rapports justes, les rapports approximatifs ou rapports abrégés, les Orientaux, dans l'espoir de trouver une base de conciliation et de réussir à anéantir la différence de théorie qu'on croit si grande, sont prêts à accepter les rapports approximatifs des intervalles. 

Si nous pensons impartialement, nous ne pouvons admettre qu'un homme, Oriental ou Occidental, voulant chanter en solo une mélodie, se serve d'un gosier sujet à des lois physiologiques différentes, selon que cet homme est né en Orient ou en Occident ! Pourquoi donc alors négliger la différence d'un comma qui existe entre les tons majeurs et mineurs, et par là, faire subir à la musique moderne des pertes si importantes au point de vue de la nuance mélodique et de l'expression? Est-ce que cette différence est vraiment inappréciable, imperceptible, comme prétendent les physiciens? Nous ne le croyons pas. 

Combien, par contre, sont significatives et dignes de longues méditations les paroles suivantes du célèbre maître qu'est M. C. Saint-Saëns : 

« Nous calculons et connaissons les commas ou neuvièmes de ton, mais nous no les utilisons pas; les demi-tons suffisent à notre organisation. Et pourtant ce n'est pas avec notre système de demi-tons et de notes synonymes que l'on peut être dans la vérité musicale. Il n'y a là qu'un à peu près, et le temps viendra peut-être où notre oreille, plus raffinée, ne s'en contentera plus. Alors un autre art naitra; l'art actuel sera comme une langue morte, dont les chefs-d'œuvre subsistent, mais qu'on ne parle plus. Ce que sera ce nouvel art, il est impossible de le prévoir; car, s'il nous apparaissait suintement, nous serions aussi incapables de l'apprécier qu'un Chinois de comprendre une symphonie de Beethoven (3). » 

M. Saint-Saëns, qui écrivait ces lignes en 1885, pense-t-il aujourd'hui que ce temps tardera à venir? Nous ne le savons pas avec certitude; s'il y a une chose dont nous soyons convaincus, c'est que le temps est venu de supprimer la phrase classique suivante qui occupe les premières pages des traités de théorie musicale publiés en Europe : « II y a deux modes en musique... » 

1. Il ne suffit pas que les instruments puissent faire seulement cette nuance; il est également nécessaire aussi qu'ils distinguent en outre le demi-ton chromatique du demi-ton diatonique. 

2. Ici je mets certainement hors de discussion le style musical, les rythmes qui sont propres à chaque nation et la manière de chanter et d'expression qui sont en rapport direct avec la langue et la nature des peuples. 

3. Cf. Harmonie et Mélodie, 4e édition, page 281, Paris, 1890

[ 2971]

Nous ne croyons pas que les oreilles des Occidentaux, qui ont fait tant de progrès dans toutes les branches des sciences et des arts, restent incapables de distinguer cette différence minime, mais de vaste conséquence; il ne leur faut pour cela qu'une rééducation et une accoutumance de l'oreille, que nous, les Orientaux, bien que restés en retard dans le domaine scientifique et artistique, nous pouvons facilement distinguer et pratiquer avec nos instruments et nos vois. 

De même, nous croyons que cet art nouveau dont parle Saint-Saëns n'est autre chose que la musique orientale. Il suffirait donc seulement que l'Occident connût mieux l'Orient musical. 

De l'opinion des Orientaux sur l'origine de la musique. — Son historique. — Quelques considérations sur l'origine commune de cet art. 

Les peuples orientaux qui ont embrassé l'islamisme admettent une origine théologique de la musique. Les anciens auteurs religieux de l'Orient citent plusieurs traditions à ce sujet, qui différent dans le détail, mais qui sont essentiellement identiques entre elles, nous préférons celle qui est la plus répandue. 

« Dieu, disent ces auteurs, après avoir créé l'univers et lui avoir donné ce degré de perfection et de magnificence qui le fit reconnaître comme l'ouvrage d'une puissance divine, ayant résolu, dans ses décrets immuables, de peupler la terre d'habitants, créa, au même moment et avant de former l'homme, toutes les limes qui, dans la suite des siècles et dans des temps déterminés, devaient animer les corps des mortels pendant la durée du monde. Après la formation de ces âmes sorties de l'immensité divine, le Créateur a ordonné que les sept planètes et autres corps célestes se missent en mouvement; les âmes ont entendu alors cette admirable harmonie qu'ils font par leurs mouvements cadencés. Parmi cette multitude innombrable d'êtres spirituels qui assistent à ce concert planétaire, les uns goûtèrent davantage le charme de ces harmonies, les autres le goûtèrent moins. Plusieurs même, mais ce ne fut que le petit nombre, y restèrent insensibles. De là vient, ajoutent les auteurs en question, le goût général de la musique chez la plus grande partie des hommes et l'aversion chez quelques-uns, qu'on peut regarder comme gens imparfaits et dénués de sentiment. » 

Telle est, selon les auteurs mystiques de l'Orient musulman, non seulement l'origine de la musique, mais encore celle des musiciens. 

Quant aux autres auteurs, surtout si nous étudions les anciens théoriciens comme Abd-uI-Kader par exemple, ils nous présentent un court résumé historique de la musique depuis Adam jusqu'à l'époque où vivait l'auteur. 

Pour en donner une idée, je traduis en partie ce résumé inédit qui est extrait d'un ouvrage' écrit par Abd-ul-Kader pour commenter le Livre des périodes de Safi-ed-din : 

« Lorsque Dieu eut créé Adam, il ordonna à l'âme d'entrer dans sou corps; et alors le pouls d'Adam se mit en mouvement. Adam avait certainement de la voix; puisque le temps qui se trouve entre les mouvements de son pouls est égal, il y avait donc dans le corps d'Adam le son et le rythme. Tout ce qu’Adam psalmodiait pour louer le bon Dieu, il le chantait à haute voix et avec une mélopée sublime. 

«  Le fils d'Adam, Chith, avait aussi une belle voix. Ce fut Lamech, fils de Gain, fils d'Adam, qui inventa le luth. Lamech avait eu une longue vie; il avait cinquante femmes et cent odalisques. Cependant il n'avait eu aucun enfant. Vers la fin de sa vie, il eut deux filles, et à l'une d'elles il donna le nom de Sala et à l'autre celui de Bem. Après quelque temps, il eut un garçon; il en ressentit beaucoup de joie et de gaieté. L'enfant était arrivé à sa cinquième année quand il mourut. Lamech pleura tellement qu'avant lui, personne au monde n'avait autant pleuré, excepté Adam lorsqu'il fut expulsé du paradis. Pour que le cadavre de son enfant fût toujours visible, Lamech le suspendit à un arbre; de temps eu temps, il allait devant lui pour déplorer sa perte. Le corps de l'enfant resta suspendu si longtemps sui- l'arbre que la chair et la peau tombèrent à terre et se détachèrent des os. Lamech coupa la branche de l'arbre à laquelle il avait pendu le cadavre, et lui donna quelque peu la forme de son fils; puis il attacha et tendit sur l’instrument en question des crins de cheval. Quand il louchait ces crins avec ses doigts, les sons produits le faisaient pleurer. Un jour, ces sons lui causèrent une telle impression qu'il mourut aussitôt. Après Lamech, la forme du luth subit des modifications et prit sa forme actuelle. L'une des deux filles de Lamech, nommée Sala, a inventé la grosse caisse. 

« Le tanbour (instrument à cordes à long manche) a été inventé par le peuple de Loth dans le but de tromper les jeunes garçons. Et les instruments à vent sont dus au peuple d'Israël, pour imiter la voix mélodieuse de David, leur prophète, qui avait apporté chez eux, comme un miracle, sa belle voix. Seulement, le nH blanc (espèce de flûte) est l'invention des Kurdes, qui l'employaient pour rappeler leurs moutons; les sons de cette flûte suffisaient pour rappeler ces animaux lorsqu'ils étaient dispersés. 

« Alexandre le Grand était très habile dans la théorie et la pratique de la musique. Pythagore, le philosophe, a beaucoup travaillé pour donner un fondement théorique à cette science. Platon est l'inventeur du Canoun (espèce de psaltérion). Aristote, lui aussi, était très habile musicien. 

« Devant notre saint prophète Mahomet, ses compagnons lisaient le Coran avec des sons mélodieux. Mahomet lui-même a loué la belle voix. Abou-Mousa-el-Echari, un des compagnons du prophète, lisait un jour le Coran chez lui avec sa voix harmonieuse; Mahomet qui passait l'écouta et ressentit une impression très douce. Une autre fois, lorsqu'il le vit, il lui raconta cette histoire. Le dévoué compagnon du prophète répondit : 

«  — Si j'avais su alors que l'apôtre de Dieu m'écoutait, j'aurais lu encore d'une façon plus attrayante. 

« La lecture du Coran se faisait, devant le prophète, dans les modes de Rahavi et de Zenguioulé. Un jour, on récita en présence de Mahomet les vers d'un poète distingué; le prophète, très impressionné par l'éloquence de cette poésie, entra dans une sorte d'extase mystique et laissa tomber son manteau : Mouavieh lui dit : 

«  — O envoyé de Dieu, comme vous dansez bien ! 

« — Ne dis pas cela, répondit Mahomet, il est injuste de ne pas vibrer lorsqu'on cite les vertus de son bien-aimé ! 

l. Le manuscrit de cet ouvrage se trouve à la Bibliothèque de Nouri-Osmanié, à Constantinople, sous le n° 3651. 

[2972]

« Farabi était très érudit dans la science musicale. II a transporté la musique, ainsi que d'autres sciences, de la langue grecque à celle des Arabes. Sur la théorie de la musique, il a écrit des traités; il était aussi bon joueur de luth. C'est lui qui a ajouté une corde à l'aigu de cet instrument. Son habileté était arrivée à un degré tel que, s'il le voulait, il pouvait faire pleurer, rire, dormir, et ensuite réveiller ses auditeurs par le son de son instrument. 

« Avicenne, qui fut aussi un savant théoricien, ayant terminé à l'âge de 17 ans l'étude de toutes les sciences de sou temps, disait pour son compte : 

« — Voilà l'homme; où sont d'autres sciences ? 

« Mais lorsqu'il essaya de s'occuper de la pratique musicale, il constata avec stupéfaction son manque d'aptitude complète et dit alors : 

« — Voilà la science; où est l'homme ?

« Avicenne n'a fait dans ses écrits que suivre le système musical de Farabi. » 

Abd-ul-Kader donne ensuite, parmi les Ommeyades et les Abassides, les noms des califes qui furent musiciens, et, pour clore cette liste, il cite les noms des principaux musiciens de profession jusqu'à son père, qui fut son maitre de musique. 

***

Si, dans l'exemplaire original, on lit le résumé historique d'Abd-ul-Kader reproduit en partie plus haut, on l'ait une remarque importante, qui consiste en ce que, parmi les musiciens cités, on trouve les noms d'artistes appartenant à divers peuples. Par exemple, à côté d'un Arabe, on cite un Turc, et à côté d'un Persan, on rencontre un Arabe. 

Cependant, si l'opinion de la plupart des auteurs européens était fondée (je ne sais trop pourquoi et comment cette opinion s'est formée), il ne devrait pas en être ainsi. Pour comprendre de quoi il s'agit, il suflit de jeter un coup d'ceil sur le texte suivant de Kiesewelter .qui se trouve à la fin de la partie historique par laquelle débute son livre Die Musik der Arabcr : 

« Ayant constaté la découverte d'un commencement de théorie musicale chez les Orientaux, dans l'entourage des califes de la dynastie des Ommeyades et plus lard de celle des Abassides, nous pouvons fixer les phases suivantes : 

« 1. — Origine et développement progressif d'une théorie propre et particulière (ni héritée, ni traditionnelle) par les philosophes arabes depuis le iiie siècle de l'hégire. Le système est celui qui admet la répartition du ton majeur en trois tons et qui donne à l'octave 17 intervalles. 

« 2. — Les grands théoriciens persans, vers la fin du viiie siècle de l'hégire, travaillent avant tout la partie mathématique avec diverses rénovations; ils partent toujours encore du vieux système arabe des dix-sept tons, et admettent les mêmes formules de tons, c'est-à-dire les gammes; ceci est l'école arabo-persane. 

«3. — Un peu plus tard (presque à la même époque), apparaît en Perse un nouveau système, sans doute transmis de l'Europe, arrangé par les Persans à la manière orientale, sans pouvoir effacer son origine européenne ; c'est le système des 7 tons avec o demitons intercalés, comme nos pianos-forte le représentent et que nous nommons le système de 12 tons. Ce système n'a jamais pu être admis dans le groupe distingué des savants persans. » 

1. Dans le langage mystique, cette expression « bien-aimé »  signifie « Dieu ». 

Les déclarations ci-dessus de Kiesewetter, qui établit trois phases dans l'histoire de la théorie de la musique chez les Orientaux, sont complètement chimériques et dénuées de tout fondement. Pour le prouver, nous répondrons point par point à ses déclarations : 

1. — Les Orientaux avouent eux-mêmes qu'ils ont emprunté aux Grecs anciens la théorie de la musique ; les ouvrages de Farabi, entre autres, contiennent à ce sujet des aveux définitifs. Donc les Orientaux n'avaient pas une théorie propre et particulière et ne devaient pas en avoir, puisque les Turcs, les Arabes et les Persans étaient, comme les autres nations, une branche de l'espèce humaine. La théorie musicale déduite par les Grecs était celle du chant humain et n'était pas seulement celle des Grecs. Il est probable que les Grecs n'avaient pas établi eux-mêmes cette théorie et qu'ils l'avaient empruntée aux Egyptiens ou à une autre nation plus ancienne. En tout cas, cette théorie était déduite de l'analyse du chant humain, et par conséquent elle était applicable à la musique de tous les peuples. D'ailleurs, les siècles ont passé, imposant beaucoup de modifications aux sciences et arts; et cependant les rapports des huit intervalles musicaux cités plus haut n'ont reçu ni changement ni perfectionnement; on constate que le chant de toutes les nations civilisées se compose de ces intervalles. 

Kiesewetter n'est pas non plus dans la vérité lorsqu'il dit que dans le système oriental, le ton majeur étant divisé en trois tons, l'octave contient 17 intervalles. Comme nous avons expliqué ce point dans les pages précédentes, nous n'entrerons pas ici dans de nouveaux détails. Nous nous contenterons d'ajouter ceci : les premières pages des traités théoriques des auteurs orientaux reproduisent une ligne droite, et sur la moitié de cette ligne on trouvera 18 signes divisant l'octave en 17 intervalles; cette ligne n'a d'autre but que de montrer comment on pourra déterminer sur une corde supposée les positions des principaux intervalles; cela ne signifie point que le nombre des sons employés dans une octave est restreint à 18. Pour en donner un exemple, la corde vide étant supposée toujours égale au ré 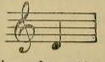  [] et étant notée avec un elif, la division de cette corde qui porte la lettre (d) donne mi#  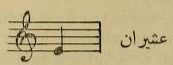  [] et les deux divisions intermédiaires portant les lettres    []  ne sont que le dièse et le bémol de ces deux notes naturelles ré-mi#. Quant aux rapports qu'il y a entre ces notes, ils sont dorénavant fixés par ces auteurs comme il suit : 

  

[]

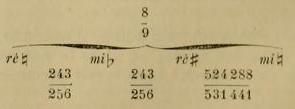On voit clairement que divisé en trois parties égales et nous répétons qu'il ne faut pas croire qu'entre ré #, et mi #, on n'emploie que ces deux notes intermédiaires.

[2673] 

Parce qu'en pratique il arrive quelquefois qu’après le ré#, la mélodie exige qu'on emploie un mi h dans le rapport d'un apotome (2048/2187) à partir du ré ; dans ce cas, il faut employer un mi b plus aigu dans le rapport d'un comma de Pythagore : 

213/256 x 524288/531441 = 2048/2187

Si nous ajoutons que les anciens théoriciens se proposaient de faire comprendre aux étudiants que, dans cette division du ton majeur, il y a cinq espèces d'intervalles différents, nous déterminerons leur pensée scolastique. 

Il y a donc : 

Voilà ce que les anciens théoriciens orientaux se sont proposé d'établir en traçant cette ligne; ils n'ont jamais pensé, comme le croient Kiesewelter et tant d'autres auteurs occidentaux, à déterminer les sons d'une gamme chromatique employée dans la pratique de la musique orientale. 

2. — Les théoriciens persans de la fin du viiie siècle de l'hégire ont beaucoup travaillé, en effet, à élargir et à détailler les œuvres de leurs devanciers. Cependant, comme Kiesewelter ne peut pas le nier, ces théoriciens ont suivi les mêmes théories. Il n'est donc pas juste de les considérer comme formant des écoles à part; les derniers ne sont que les commentateurs des premiers. 

3. — L'allégation de Kiesewelter d'après laquelle il apparaîtrait alors en Perse un système semblable au système moderne de 12 tons modérés, n'est que pure invention. Aucun document ne permet de la démontrer; elle n'est qu'une hypothèse construite par Kiesewetter pour donner une base à ses idées préconçues. 

***

On peut facilement deviner l'étal d'esprit d'un Oriental qui, ayant lu seulement l'opinion de ses compatriotes sur l'origine théologique de la musique, el s'étant ainsi habitué à considérer la musique comme un don divin à tous les hommes, prend pour la première fois connaissance des textes des auteurs occidentaux concernant les diverses manifestations de l'art musical chez les différents peuples. 

C'est ce qui m'est arrivé. Au temps où le cercle de mes études était exclusivement borné aux traités orientaux et où je n'avais pas encore appris le français, je ne concevais nullement que les Européens, qui ont réalisé d'immenses progrès dans le domaine scientifique el artistique, pussent se contenter, en musique, de deux modes, el cela sans motif pour cette préférence, alors que tant de modes, ayant chacun une couleur et une saveur spéciales, sont depuis longtemps en usage en Orient. De même, je ne m'imaginais pas qu'ils pussent regarder comme un art étrange la musique des Orientaux, qui, tout en employant les deux modes des Occidentaux, a en outre réussi à conserver les autres modes si sublimes de l'antiquité, et voir la cause de cette diversité dans « le caractère sensuel des petits intervalles de son, et dans le rapport de ce caractère avec l'organisation physique des peuples de l'Asie (1). »

Or, au point de vue de l'organisation physique, nous ne constatons aucune différence entre les Orientaux et les Occidentaux, el en outre, nous savons que la musique orientale n'emploie pas d'intervalles plus petits que ceux de la musique occidentale. En effet, comme nous l'avons dit plus haut, le plus petit intervalle en usage chez les Orientaux est le limma 243/256 ; quant au plus petit intervalle de la musique européenne, c'est — d'après les physiciens occidentaux eux-mêmes — le demi-ton mineur, qui est représenté par le rapport de 24/25, certainement un peu plus petit que 243/256.  Il en résulte donc encore que l'allégation de l'emploi des petits intervalles n'est pas juste. 

On pourra penser que ces détails ne sont pas ici à leur place; cependant, notre but, en les donnant, est de préparer un terrain pour appuyer notre idée : 

Je sais bien qu'on trouve en Europe peu de personnes qui prennent au sérieux la tradition des Orientaux sur l'origine théologique de la musique. Nous, les Orientaux, nous n'avons pas la prétention de blâmer les convictions d'autrui, mais nous constatons que, chez les Occidentaux, certaines idées qui ne sont pas très en désaccord avec la tradition orientale se sont fait jour sur ce point. Il y a seulement cette différence que la même vérité se présente, d'un côté, avec les formes luxuriantes de l'imagination orientale, et de l'autre dans la langue plus sérieuse et dans la pensée plus concrète de l'Occident. 

Luther dit : « La musique est un don de Dieu. » Mme Cottin écrit : « La musique est comme une langue universelle qui raconte harmonieusement toutes les sensations. » En parlant ainsi, ces auteurs n'ont pas fait autre chose que d'accepter l'origine théologique de la musique. 

Alfred de Musset dit plaisamment de son côté : « C'est la musique, moi, qui m'a fait croire en Dieu; » et l'Encyclopédie Larousse, en reproduisant cette parole du grand poète français, ajoute qu'en la prononçant, « Musset est à la fois très vrai et très profond ». 

Mais laissons de côté toutes ces citations, et disons tout simplement que « la musique, innée chez l'homme, comme le sentiment delà parole, n'a point eu, à proprement parler, d'origine. » Nous croyons que cette thèse ne sera contestée par personne, puisqu'elle est la plus généralement acceptée par les Occidentaux et les Orientaux. Faisons une nouvelle concession, et disons provisoirement que la musique occidentale et la musique orientale sont deux musiques à part, très distinctes l'une de l'autre, comme les deux langues de deux peuples d'origine différente. Arrivé à ce point, nous pouvons émettre ce vœu, qui n'est que très logique : de même qu'un peuple apprend la langue d'un autre peuple, de même, Orientaux et Occidentaux devraient apprendre la musique les uns des autres; on comprendrait alors de part et d'autre que la différence imaginée n'existe qu'en apparence.

1. Cf. Fétis, ouvrage cit., tome II, pages 370 et 371. 

[2974]

Dans ce cas, la tâche de chacun serait bien claire et bien simple : de même que les langues empruntent aux autres langues les mots qui n'existent pas dans leur vocabulaire, de même, les Occidentaux emprunteraient les divers modes qui ne sont pas officiellement acceptés par la musique moderne, et les Orientaux, à leur tour, s'empresseraient de profiter des progrès réalisés dans le domaine musical par les Occidentaux; en un mot, si, en musique, l'Orient et l'Occident se connaissaient mieux, nombre de volumes écrits jusqu'à présent sur de pures hypothèses apparaîtraient comme n'ayant aucune valeur scientifique, et tout le monde y gagnerait. C'est notre souhait le plus vif, et nous serions vraiment heureux si cette modeste étude posait la première pierre du monument qui porterait le nom d’ « union musicale entre l'Orient et l'Occident ». 

 *
**

Après la lecture du chapitre précédent, une objection peut nous être faite : 

«  Puisqu'on reconnaît que la musique est un don fait par Dieu aux hommes, que faut-il penser de la différence de système qui existerait, si on croit certains auteurs, entre les musiques des différents peuples? Puisque tous les peuples sont les créatures de Dieu, ne serait-il pas plus naturel que les notes qui entrent dans la composition du chant humain eussent partout entre elles les mêmes rapports musicaux ? »

Les musicologues occidentaux qui ont étudié cette question, prenant en considération, avant tout, les nations non civilisées et sauvages, s'expriment ainsi : 

« La musique des Européens paraîtrait monstrueuse à d'autres peuples, dont le système musical et, par conséquent, la tonalité reposent sur des bases absolument différentes. Par contre, la musique de ces peuples produirait sur nos oreilles l'effet d'une terrible cacophonie. D'où on doit conclure que, si le son est dans la nature, l'ordre de succession des différents sons pour arriver à la constitution d'une gamme, d'un système, est un fait arbitraire, qui dépend uniquement de la volonté humaine ou même de son caprice, et qui ne devient une loi que par l'habitude. 

« Entre un son donné et sa reproduction à l'aigu (octave), il n'est aucun point intermédiaire qui ne puisse être considéré comme la place d'un intervalle. Tous les intervalles étant dans la nature, on peut procéder par ton, par demi-ton, tiers, quart, cinquième ou dixième de ton, et cette façon de procéder n'a de bornes que la faculté pour l'oreille de percevoir et d'apprécier l'intervalle qui sépare deux sons. Dans cet ordre d'idées, tout dépend de l'habitude et de l'éducation. » 

Si on désire se faire une idée juste de cette question, il faut, avant tout, spécifier ce qu'on entend par nations non civilisées. Quelles sont ces nations? Ce sont celles qui n'ont ni art ni science, qui ne savent ni lire ni écrire et qui vivent à l'état plus ou moins sauvage. Examinons une d'entre elles. De ce que, chez elle, on aura percé un roseau au hasard, pour en tirer des sons quelconques, et de ce que, en accompagnant ces sons sur une peau tendue, on aura donné satisfaction aux auditeurs, s'ensuit-il que nous avons là une musique, un système musical, une tonalité?  Nous ne le pensons pas. 

Dans une autre nation, au contraire, si les arts et les sciences sont déjà cultivés, l'attention se portera aussi sur la musique, et la musique sera l'objet de traités spéciaux qui en expliqueront la théorie et la pratique. 

Ce sont seulement les musiques des nations arrivées à ce degré de progrès intellectuel, arrivées à l'état d'art codifié, qui peuvent être étudiées scientifiquement. 

En les étudiant, nous voyons que les lois naturelles en musique sont strictement observées par tous les peuples civilisés sans exception. Par exemple, pour avoir l'octave d'une note qui est donnée par la longueur totale d'une corde tendue, un Persan et un Japonais agissent de môme façon, et trouvent cette octave au milieu de la corde. De même, si un Chinois prend le 1/3 d'une corde pour obtenir la quinte du son donné par la corde libre, un Européen doit faire la même opération dans le même but. 

Cette coïncidence du sentiment musical ne se manifeste pas seulement pour Voctave et la quinte ; les huit intervalles (1), y compris l'octave et la quinte, sont tous observés instinctivement chez les diverses nations par des chanteurs qui n'ont que des idées très sommaires sur la nature et la valeur mathématique des intervalles. 

Par conséquent, se basant sur ce fait qu'entre un son donné et son octave on peut intercaler théoriquement plusieurs sons, et que de la sorte on peut concevoir des systèmes de sons composés d'intervalles indéfinis et placés à des degrés indéterminés, il n'est pas exact de conclure que chaque peuple a choisi les sons qui lui paraissaient convenables pour composer son système musical; il ne faut pas oublier que les systèmes ne sont pas le résultat de conceptions d'un homme ou d'un théoricien; le rôle de celui-ci est d'examiner les laits et d'en tirer la théorie. 

Si la musique des Européens parait quelque peu incompréhensible aux Orientaux, cela tient à deux raisons : 1° les intervalles faux de la gamme tempérée qui choquent leurs oreilles; 2° leur manque d'habitude d'entendre les sons harmonisés. D'ailleurs, rien d'étonnant à cela : si Lully était ramené aujourd'hui à la vie, il ne comprendrait pas plus que les Orientaux les compositeurs européens de notre temps qui, dans le désir de trouver de nouvelles formes et des effets originaux, emploient dans leurs œuvres des bizarreries si compliquées. 

D'autre part, si la musique orientale paraît étrange aux Européens, cela provient de ce qu'ils n'ont : 1° entendu depuis l'enfance que des sons tempérés et harmonisés; 2° de ce qu'ils ne sont pas habitués à distinguer d'autres modes que les deux modes majeur et mineur. 

D'après les paroles des musicologues occidentaux rapportées plus haut, le son étant dans la nature, le choix fait entre les sons pour former une gamme serait arbitraire, et ne deviendrait une loi que par l'habitude. 

Nous pensons tout autrement, parce que s'il en était ainsi, il serait possible d'habituer l'oreille à n'importe quelle série de notes dont les intervalles seraient constitués au hasard d'après des rap[)orts non musicaux. Pour donner un exemple, je forme arbitrairement une série de huit sons pouvant former une gamme et dont les nombres de vibrations sont les suivants : 

1. Ces huit intervalles sont : l'octave, la quinte, la quarte, la tierce, le ton majeur, le ton mineur, l'apotome et le limma. 

[2975]

Accordons les cordes d'un piano pour réaliser strictement cette gamme. Maintenant je vous laisse libre plusieurs années; répétez ces sons des milliers de fois. Est-ce que votre oreille trouvera quelque plaisir à les entendre, et surtout arriverez-vous jamais à les faire chanter à un artiste ? Certainement non!... 

Donc, il faut reconnaitre que les huit principaux intervalles musicaux mentionnés plus haut et qui forment les bases rationnelles de tout système musical, soit oriental, soit occidental, sont donnés par la nature à chaque homme doué du goût mélodique; que si les différents peuples ont adopté dans leurs chants certaines dispositions de ces intervalles principaux pour en former différentes gammes, ce n'est que le résultat du rapport du caractère de ce peuple avec la nature de ces gammes, et que les diverses gammes qu'on rencontre dans le chant des différents peuples sont praticables par tous les hommes cultivés, sans distinction de race et d'origine, puisqu'elles sont toutes données par la nature, qui est la seule et commune source à laquelle s'adressent les hommes pour puiser les formes mélodiques propres à la traduction de leurs sentiments. 

>> Lire la suite